Расчетные формулы

Схема единственного деления

Делим первое уравнение этой системы на коэффициент a₁₁ ¹ 0 при неизвестном х₁ (ведущий элемент).

Выполнения условия a₁₁¹ 0 можно добиться всегда путем перестановки уравнений системы.

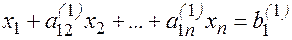(3) или

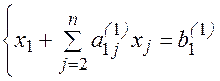
Исключаем неизвестное х₁ из остальных уравнений системы (для этого достаточно из каждого уравнения ( i =2,3,…,n) вычесть уравнение (3), предварительно умноженное на коэффициент при х₁, т.е. на a₂₁, a₃₁ и т.д. a_i1,

Например:

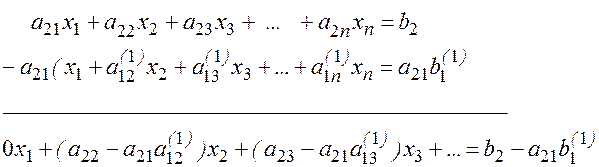
Обозначим

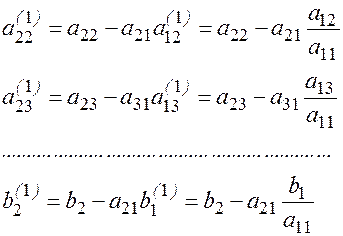
Преобразованные уравнения будут иметь вид:

.................

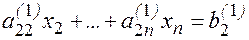
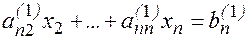
Здесь обозначено

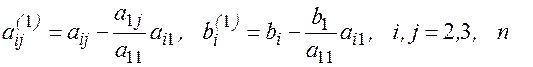
Матрица системы имеет вид: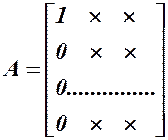

Вслед за этим, оставив первое уравнение в покое, над остальными уравнениями системы совершим аналогичные преобразования:

1. выберем из их числа уравнение с ведущим элементом a₂₂⁽¹⁾

2. и исключим с его помощью из остальных уравнений неизвестное х₂.

3. Повторяя этот процесс n раз, вместо системы (2) получим равносильную ей систему с треугольной матрицей:

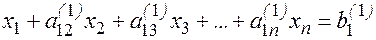
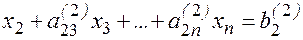(4)

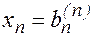
Матрицы такого вида называются верхними треугольными матрицами.

Из системы (4) последовательно находятся значения всех
неизвестных x_n, x_n-1,..., x₁.

Таким образом, процесс решения (1) по методу Гаусса распадается на два этапа. Первый этап, состоящий в последовательном исключении неизвестных, называют прямым ходом. (число арифметических действий ¸ 2N³/3)

Обратным ходом. (число арифметических действий ¸ N²)

Общие формулы обратного хода имеют вид:

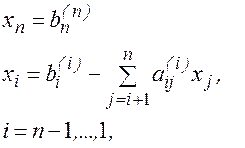
ПРЯМОЙ ХОД:

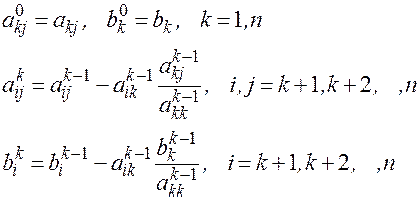(7)

ОБРАТНЫЙ ХОД:

(8)

Основным ограничением метода является предположение о том, что все элементы 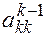, на которые проводится деление, отличны от нуля. Число 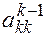называется ведущим элементом на к – том шаге исключения.

Полезно после определения x_i вычислить невязки

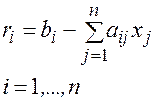
Невязка – это количественная мера несоответствия между правыми и левыми частями уравнений системы при подстановке в них вычисленного решения.

Так как реальные машинные вычисления производятся не с точными, а с усеченными числами, т.е. неизбежны ошибки округления, то анализируя, например, формулы прямого хода, можно сделать вывод о том, что выполнение алгоритма может прекратиться или привести к неверным результатам, если знаменатели дробей на каком – то этапе окажутся равными нулю или очень маленькими числами.

Чтобы уменьшить влияние ошибок округления и исключить деление на нуль, на каждом этапе прямого хода уравнения системы обычно переставляются так, чтобы деление производилось на наибольший по модулю в данном столбце элемент. Числа, на которые производится деление в методе Гаусса, называются ведущими или главными элементами. Отсюда название модификации метода, исключающей деление на нуль и уменьшающей вычислительные погрешности, метод Гаусса с выбором главного элемента (оптимальный метод Гаусса).

Дата добавления: 2014-12-07