Основные понятия теории разностных схем

ЛЕКЦИЯ № 14

Пусть на некотором отрезке D поставлена некоторая дифференциальная краевая задача.

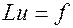, (1)

L - заданный дифференциальный оператор, f - заданная правая часть.

Будем предполагать, что решение u з адачи (1) на отрезке существует.

На отрезке D конечное число точек, ,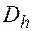

Заменяем u(x) à таблицей значений этого решения в
точках сетки .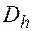

Предполагается, что сетка 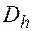зависит от параметра h>0.

Например, можно положить h=1/N, где N - некоторое натуральное число, и принять за сетку 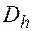совокупность точек .

Искомая сеточная функция в этом случае в точке сетки 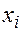принимает значения , которое будем обозначать .

. (2)

Назовем ее разностной краевой задачей (разностной схемой).

Определение 1.

Будем говорить, что решение разностной краевой задачи (2) при сгущении сетки сходится к решению u дифференциальной краевой задачи (1), если

.

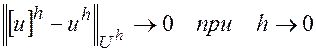Если, сверх того, выполнено неравенство

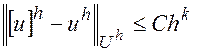(3)

где С>0, k>o – некоторые постоянные, не зависящие от h, то будем говорить, что имеет место сходимость порядка h^k или что разностная схема имеет k -й порядок точности.

В этом определении - проекция точного решения задачи (1) на сетку ( 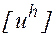- сеточная функция, компоненты которой есть значения точного решения в
узлах сетки).

Предположим, что разностная задача (2) имеет единственное решение .

Если бы при подстановке в левую часть (2) вместо сеточной функции (проекции точного решения на сетку) равенство (2) оказалось бы в точности выполненным, то ввиду единственности решения имело бы место равенство = , идеальное с точки зрения сходимости.

Это означало бы, что решение разностной задачи (2) совпадает с искомой сеточной функцией , которую мы условились считать точным решением.

Однако, как правило, систему (2) не удается выбрать так, чтобы в точности ей удовлетворяла.

При подстановке в уравнение (2) возникает некоторая невязка:

Если эта невязка 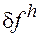стремится к нулю при , так что удовлетворяет уравнению (2) все точнее, то будем говорить:

Определение 2.

Будем говорить, что разностная схема (2) аппроксимирует исходную дифференциальную задачу (1) на решении u, если

Если, сверх того, имеет место неравенство

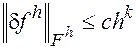(4)

где С>0, k>o – некоторые постоянные, не зависящие от h, то будем говорить, что имеет место аппроксимация порядка h^k или порядка к относительно величины h.

В случае аппроксимации можно считать, что уравнение (3) которому удовлетворяет , получается из уравнения (2) путем прибавления к правой части некоторой малой (при малом h) добавки .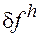

Следовательно, если решение задачи (2) устойчиво относительно возмущения правой 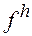, т.е. мало изменяется при малом изменении правой части, то решение задачи (2) и решение задачи (3) отличаются мало, так что из аппроксимации

при следует сходимость

, при

Определение 3.

Будем называть разностную схему (2) устойчивой, если существуют такие постоянные h₀ и d ₀, что при любом h<h₀ и любой сеточной функции e_рÎF_h, такой, что

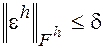разностная задача

,

полученная из (2) добавление к правой части возмущения e^h имеет место и имеет только одно решение z^h, причем справедлива оценка

, (5)

где С₁ – некоторая постоянная, не зависящая от h.

Последнее неравенство означает, что малое возмущение e^h правой части разностной схемы (2) вызывает равномерно относительно h малое возмущение (z^h-u^h) решения u^h.

Определение 4.

Будем называть разностную схему (2) с линейным оператором L_hустойчивой, если при любой правой части f_hÎF_h уравнение имеет единственное решение u_hÎU_h, причем

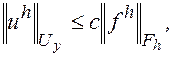(6)

где С – некоторая постоянная, не зависящая от h.

Можно показать, в случае линейности разностного оператора L_h определения устойчивости 3 и 4 равносильны.

Теорема 1 (теорема Лакса о сходимости).

Пусть разностная схема (2) аппроксимирует задачу (1) на решении u с порядком h^k и устойчива.

Тогда решение разностной задачи сходится к решению дифференциальной задачи 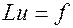, причем имеет место оценка

,

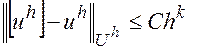где С – некоторая постоянная, не зависящая от h.

Эта теорема позволяет свести вопрос о важнейшей с практической точки зрения проблеме исследования сходимости к вопросу исследования аппроксимации и устойчивости.

Доказательство:

Положим и . Тогда определение устойчивости (5)

примет вид, (привлекая условие (4))

Дата добавления: 2014-12-07