Основные определения. Ти точечная разностная схема (повышенного порядка точности)

Ти точечная разностная схема (повышенного порядка точности).

Пятиточечная разностная схема.

(1)

i=1,..., n-1; j=1,..., n-1

Погрешность аппроксимации разностного уравнения составляет О(h²+k²).

Уравнение (1) вместе со значениями U_i,j в граничных узлах образуют систему алгебраических уравнений относительно приближенных значений функции U(x,y) в узлах сетки (x_i,y_j).

Наиболее простой вид имеет эта система при h=k:

U_i0=f₃ (x_i), U_im=f₄ (x_i), U_0j=f₁ (y_j ), U_nj=f₂ (y_j ), i=1,..., n-1; j=1,..., m-1

Погрешность аппроксимации разностной схемы О(h⁴+k⁴), на квадратной сетке О(h⁶),

3. Так как оператор Лапласа инвариантен относительно поворота системы координат, то на квадратной сетке можно вместо использовать диагональные узлы. Шаг сетки увеличится до Ö2 h.

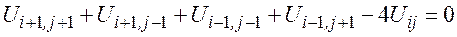
Погрешность аппроксимации разностной схемы О (h²).

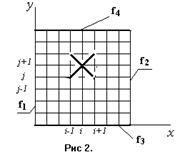
Для определения величин U_i,j требуется решить систему линейных алгебраических уравнений Методы решения разделяются на прямые и итерационные.

Прямые методы: Метод Гаусса и его модификации, прогонки.

Итерационные методы: метод итераций, метод Зейделя

Итерационный метод Зейделя:

где верхний индекс s - номер итерации. При последовательность
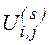сходится к точному решению системы.

В качестве условия окончания итерационного процесса можно принять .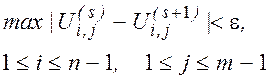

Погрешность приближенного решения, получаемого конечно- разностным методом, складывается из двух погрешностей: погрешности аппроксимации дифференциального уравнения разностным и погрешности итерационного процесса.

Говоря нестрого, граф — это множество точек (вершин) и соединяющих их криволинейных отрезков (ребер). Типичный пример графа — схема каких-либо транспортных путей, например, автомобильных дорог. Пункты назначения — это вершины графа, а соединяющие их дороги — ребра. Возникают задачи поиска пути в графе, обладающего тем или иным свойством. Например, можно требовать, чтобы каждое ребро проходилось не более одного раза; можно — чтобы каждая вершина. Можно каждому ребру сопоставить положительное число (длина дороги), и заниматься поисками кратчайшего пути от одного пункта до другого.

В ряде случаев ребру графа придается направление, то есть одна из двух точек, которые это ребро соединят, считается начальной, а другая – конечной. Так, например, естественно поступить, если ребро изображает дорогу с односторонним движением. Направление ребра изображается стрелкой. Граф с направленными ребрами называется ориентированным. Если направления ребер не фиксируются, то граф называется неориентированным. Не исключено также, что одна пара вершин соединена несколькими ребрами (такие ребра называются кратными) или одно ребро соединяет вершину с самою собой (такое ребро называется петлей). Некоторые вершины могут вообще ни с какими другими вершинами не соединяться ребрами — такие вершины называются изолированными.

Рис. 1 Рис. 2

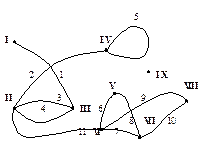На рис.1 изображен неориентированный граф, вершины которого обозначены римскими цифрами, а ребра — арабскими. Ребра 3 и 4 являются кратными — они соединяют вершины II и III. Ребро 5 является петлей. Вершина IX — изолированная. Заметим, что ребра 2 и 1, 9 и 8 пересекаются на рисунке, но точки их пересечения не являются вершинами графа. (Вопрос о том, можно ли изобразить на плоскости граф так, чтобы его различные ребра не пересекались, будет рассмотрен в § 14). На рисунке 2 изображен ориентированный граф. Он также имеет кратные ребра (1 и 2), петлю (3), изолированную вершину (VI).

Дадим теперь точные определения.

Графом называется пара (V, Е), где V — множество вершин, Е — множество ребер. Мы будем рассматривать только конечные графы, то есть множества V и Е будем считать конечными. Если ребро е соединяет вершины v₁ и v₂, то будем говорить, что е инцидентно вершинам v₁ и v₂, и наоборот, что каждая из вершин v₁, v₂ инцидентна ребру е. Иногда ребро е, соединяющее вершины v₁ и v₂, удобно обозначать парой (v₁, v₂), причем, если граф ориентирован, то пара (v₁, v₂) считается упорядоченной, вершина v₁ называется началом ребра, а v₂ — концом. Если же граф не ориентирован, то порядок элементов в паре (v₁, v₂), обозначающей ребро, не существенен.

Граф H называется частью графа G, если множество вершин H содержится во множестве вершин G, а множество ребер H — во множестве ребер G. Если при этом множество вершин H совпадет с множеством вершин G, то H называется суграфом или остовом графа G. Если H содержит все ребра графа G, соединяющие вершины, принадлежащие множеству вершин H, то H называется подграфом графа G.

Дата добавления: 2014-12-07