Изоморфизм графов

Пусть G(V, Е) и G’ = (V’, Е’) – два графа. Скажем, что эти два графа изоморфны, если существует пара биективных отображений j: V ®V’, y: Е®Е’ таких, что для любого ребра е = (v₁, v₂)ÎЕ y (е) = (j (v₁), j (v₂)). Иными словами, отображение y переводит ребро, соединяющее две вершины, в ребро, соединяющее образы этих вершин при отображении j.

Изоморфными могут быть на первый взгляд непохожие друг на друга графы.

Примеры. 1

Изоморфизм этих двух графов задается отображением вершин j: x_i®у_i, i =1,2,3,4; ребро (х_i, х_j) переводится отображением y в ребро (у_i,у_j). Заметим, что данные графы являются полными, то есть вместе с любыми двумя вершинами содержат единственное соединяющее их ребро. Полные графы с n вершинами обозначаются K_n. Ясно, что любые два полных графа с одинаковым количеством вершин изоморфны.

Изоморфизм этих двух графов зададим отображением вершин с помощью подстановки:

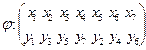
(вершина х_i переходит в вершину у _i расположенную под ней; ребро (х_i, х_k) переходит в соответствующее ребро (у_j, у_l), где х_i переходит в у_j, а х_k — в у_l). Как устроен этот изоморфизм ясно: семиугольник с вершинами х₁,…,х₇ переходит в ломаную, составленную из диагоналей семиугольника с вершинами у,…,у; наоборот — диагонали семиугольника слева переходят в стороны семиугольника справа.

Ясно, что у изоморфных графов должно быть одинаковое число вершин и ребер. Однако этого условия не достаточно для изоморфизма. Пусть, например, последовательность ребер образует цикл, то есть конец каждого предыдущего ребра является началом последующего и конец последнего ребра совпадает с началом первого; число ребер последовательности называется длиной цикла (точные определения см. в § 5). Очевидно, при изоморфизме цикл переходит в цикл той же длины. Значит, у изоморфных графов должно быть одинаковое число циклов определенной длины. Следующие два графа

неизоморфны, так как у одного из них два цикла длины 4, а у другого – один.

Дата добавления: 2014-12-07