График выполнения и сдачи заданий СРС 2 страница

2. В колоде 32 карты. Наугад вынимают 5 карт. Найти вероятность того, что среди них окажется хотя бы одна дама.

3. Произведен залп из двух орудий. Вероятность попадания в цель из первого орудия равна 0,8, из второго - 0,9. Найти вероятность поражения цели.

4. Вероятность появления событий в каждом из 10000 независимых испытаний постоянна и равна 0,8. Найти вероятность того, что события произойдет не более 7400 раз.

5. Вероятность выигрыша по облигации займа равна 0,25. Какова вероятность того, что из 8 облигаций 3 выиграют?

6. Вероятность наступления события А в одном опыте равна 0,6. Найти вероятность того, что событие А наступит 1400 раз в 2400 опытах.

7. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины, заданной законом распределения:

Х
р	0,2	0,3	0,5

8. Случайная величина 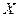задана функцией распределения:

Найти: а) плотность распределения случайной величины; б) вероятность того, что в результате испытания величина примет значение, заключённое в интервале .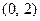

9. Задана плотность распределения непрерывной случайной величины :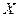

Найти функцию распределения .

Индивидуальное домашнее задание №2

I. Составьте логическую схему базы знаний по темам курса и перечень основных зависимостей и формул.

II. Решите самостоятельно следующие задачи. Данные своей задачи возьмите по номеру, соответствующему вашему порядковому номеру.

1. Из таблицы 1 чисел выборки из равномерного распределения на отрезке [0,100] возьмите подряд 100 чисел, начиная с номера 4 N, где N – ваш порядковый номер в списке группы (дойдя до конца таблицы, перейдите в её начало). Возьмите в качестве интервалов группировки интервалы (0,20), (20,40) …. (80,100) и напишите таблицу эмпирического распределения для этих интервалов. По этой таблице постройте гистограмму и полигон, сосчитайте эмпирическое среднее, дисперсию (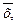 S²), эмпирическое среднеквадратическое отклонение. Выпишите теоретические значение для этих величин и сравните их с эмпирическими.

Таблица 1.

Последовательность случайных чисел,

распределенных равномерно на отрезке [0,100]

2. Из таблицы 2 чисел выборки из нормального распределения N(0,1) возьмите подряд 100 чисел, начиная с номера 4 N, где N – ваш порядковый номер в списке группы (дойдя до конца таблицы, перейдите в её начало). Возьмите в качестве интервалов группировки интервалы (-3,-2), (-2,-1) … (2,3) и напишите таблицу эмпирического распределения для этих интервалов. По этой таблице постройте гистограмму и полигон, сосчитайте эмпирическое среднее, дисперсию (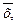 S²), эмпирическое среднеквадратическое отклонение. Выпишите теоретические значение для этих величин и сравните их с эмпирическими.

Таблица 2.

Последовательность случайных чисел,

имеющих распределение N(0,1)

0,414	0,011	0,666	-1,132	-0,410	-1,077	1,484	-0,340	0,789	-0,494
0,364	-1,237	-0,044	-0,111	-0,210	0,931	0,616	-0,377	-0,433	1,048
-0,037	0,759	0,609	-2,043	-2,290	0,404	-0,543	0,486	0,869	0,347
2,816	-0,464	-0,632	-1,614	0,372	-0,074	-0,916	1,314	-0,038	0,673
0,563	-0,107	0,131	-1,808	0,284	0,458	1,307	-1,625	-0,629	-0,504
-0,056	-0,131	0,048	1,879	-1,016	0,360	-0,119	2,331	1,672	-1,053
0,840	0,246	-0,237	-1,312	1,603	-0,952	-0,566	1,600	0,465	1,931
0,110	0,251	0,116	-0,957	-0,190	1,479	-0,986	1,249	1,934	0,070
-1,358	-1,246	-0,959	-1,297	-0,722	0,925	0,783	-0,402	0,619	1,826
1,272	-0,945	0,494	0,050	-1,696	1,876	0,063	0,132	0,682	0,544
-0,417	-0,666	-0,104	-0,253	-2,543	-1,133	1,987	0,668	0,360	1,927
1,183	1,211	1,765	0,035	-0,359	0,193	-1,023	-0,222	-0,616	-0,060
-1,319	-0,785	-0,430	-0,298	0,248	-0,088	-1,379	0,295	-0,115	-0,621
-0,618	0,209	0,979	0,906	-0,096	-1,376	1,047	-0,872	-2,200	-1,384
1,425	-0,812	0,748	-1,095

3. В условиях предыдущей задачи построить 95%-ый доверительный интервал для математического ожидания генеральной совокупности при условии, что дисперсия генерального распределения известна и равна 1.Попало ли оцениваемое значение в доверительный интервал?

4. То же задание, что и в задаче 3, но считать, что дисперсия генерального распределения неизвестна. Попало ли оцениваемое значение в доверительный интервал? Сильно ли различаются интервалы, построенные в 3 и 4 задачах?

5. Производительность стальных канатов долгое время обеспечивал прочность каната на разрыв μ=55000 кг при стандартном отклонении

σ = 500кг. После усовершенствования процесса изготовления, производитель стал утверждать, что прочность каната на разрыв возросла. При испытании выборки из п=50 канатов получено, что средняя выборочная прочность составляет 55250 кг. Заказчик решил проверить гипотезу Н₀: μ=55000 при уровне значимости 0,05 (так как он сомневается в увеличении μ). Пройдет ли эта гипотеза?

Список литературы

Основная:

1. Гмурман, В.Е. Теория вероятностей и математическая статистика [Текст]: Учебное пособие. -12-е изд., перераб.. -М.: Высш.образование, 2006.

2. Ермаков В.И. Общий курс высшей математики [Текст]. Учебник.–М.: ИНФРА-М, 2003., 2005, 2008 – 656 с.

3. Кремер, Н.Ш. Теория вероятностей и математическая статистика [Текст]: Учебник.-2-е изд., перераб. и доп.- М.: ЮНИТИ, 2006.-573 с.- Гриф МО

4. Сборник задач по высшей математике для экономистов [Текст]: учебное пособие/ Под ред. В. И. Ермакова.- 2-е изд, испр.- М.: Инфра - М, 2010.- 575 c.

5. Тырсин, А.Н. Математика. Теория вероятностей и математическая статистика [Текст]: учеб. пособие. Челябинск: Челяб. гос.ун-т,2007.235с.

Дополнительная:

1. Бачурин, В.А. Сборник задач по математике [Текст]: учебное пособие/ В.А. Бачурин, 2009.

2. Вентцель, Е.С. Задачи и упражнения по теории вероятностей [Текст]: учебное пособие: Учебное пособие/ Е.С. Вентцель.- 5-е изд., испр.- М.: Академия, 2004.- 440 c.

3. Вентцель, Е.С. Теория вероятностей [Текст]. –М.: Издательский центр «Академия», 2005.-576 с. Палий И.А. Введение в теорию вероятностей. Учебное пособие. М.: Высш.шк., 2005.-175 с

4. Высшая математика для экономистов [Текст]: Учебник /под ред. Н.Ш. Кремера.- 3-е изд.- М.: ЮНИТИ-ДАНА, 2007.- 479 с.- Гриф МО

5. Высшая математика для экономических специальностей [Текст]: учебник/ Б.А. Путко, И.М. Тришин/ под ред. Н.Ш. Кремера.- 2-е изд., перераб. и доп.- М.: Высш. образование, 2009.- 893 c.

6. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике [Текст]: учебное пособие/ В.Е. Гмурман.- 12 изд., перераб.и доп..- М.: Высш.образование, 2006.- 404 c.

7. Ивченко, Г. И. Задачи с решениями по математической статистике [Текст]:Учебное пособие.- 2-е изд., испр., и доп.- М.: Дрофа, 2007.- 318 с.-

8. Красс, М.С., Чупрынов Б.П. Математика для экономистов [Текст]: учебное пособие/ М.С. Красс, Б.П. Чупрынов: Питер, 2010: ил.- (Учебное пособие).

9. Луканкин, Высшая математика для экономистов [Текст]: учебное пособие/ Г.Л. Луканкин, А.Г. Луканкин.- 999.- М.: Экзамен, 2009.- 285 c.

10. Макаров, С.И. Математика для экономистов [Текст]: электронный учебник/ С.И. Макаров.- М.: Кнорус, 2010.

11. Малугин, В.А. Математика для экономистов [Текст]: учебник/ В.А. Малугин, 2008.

12. Теория вероятностей: Электронная библиотека (CD - ROM)

13. Шамолин, М.В. Высшая математика [Текст]: учебник/ М.В. Шамолин.- М.: Экзамен, 2009.- 909 c.

14. Шипачев, В. С. Задачник по высшей математике [Текст]: учебное пособие/ В. С. Шипачев, 2008.

Методические указания по СРС для студентов заочной формы обучения на базе среднего, среднего профессионального и высшего образования.

Необходимо выполнить задания 1-5 из раздела «Теория вероятностей» и задания 1-5 из раздела «Математическая статистика». При оформлении и выполнении индивидуального домашнего задания необходимо соблюдать следующие правила:

1. В начале работы (на обложке) должны быть ясно написаны фамилия студента, его инициалы, группа.
2. Контрольная работа выполняется в учебной тетради синей пастой.
3. Решения задач необходимо сопровождать подробными пояснениями.
4. ИДЗ, выполненное не по своему варианту, не зачитывается.

Студент должен выполнять задания по варианту, номер которого совпадает с его номером студента в списке группы.

Индивидуальное домашнее задание

Раздел «Теория вероятности»

I. Решите самостоятельно следующие задачи. Данные своей задачи возьмите из таблицы по номеру, соответствующему вашему порядковому номеру.

1. Из В1 билетов лотереи В2 выигрышных. Наугад берут 2 билета. Какова вероятность того, что они выигрышные?

2. Вероятность того, что студент сдаст первый экзамен равна Р1, вероятность сдачи второго экзамена Р2, третьего – Р3. найти вероятность того, что

a) Студент сдаст хотя бы один экзамен;

b) Студент сдаст только один экзамен;

c) Студент сдаст все три экзамена;

d) Студент не сдаст ни одного экзамена.

3. Два охотника увидели волка и одновременно в него выстрелили. Каждый охотник попадает с вероятностью р. Найти вероятность того, что

a) Волк будет подстрелен;

b) В волка попадет только один охотник.

4. Получена партия телевизоров, из которых Т% сделаны на одном заводе, а остальные на втором. Вероятность брака на первом заводе равна р1, а на втором – р2. найти вероятность того, что

a) Случайно выбранный телевизор не имеет брака;

b) Телевизор изготовлен на первом заводе, если известно, что он не бракованный.

5. При работе ЭВМ число сбоев подчиняется закону Пуассона. Среднее число сбоев в неделю равно λ найти вероятность того, что в течение данной недели

a) не будет ни одного сбоя;

b) будет только один сбой;

c) будет более трех сбоев.

Данные к задачам 1-5

	№1	№2	№3	№4	№5
	В1	В2	Р1	Р2	Р3	Р	Т	р1	р2	λ	S
0.			0,9	0,8	0,7	0,6		0,01	0,1
1.			0,3	0,4	0,3	0,25		0,10	0,03
2.			0,6	0,4	0,3	0,26		0,11	0,04
3.			0,7	0,4	0,3	0,27		0,12	0,05
4.			0,8	0,4	0,3	0,28		0,01	0,06
5.			0,9	0,4	0,3	0,29		0,01	0,07
6.			0,6	0,5	0,3	0,30		0,01	0,08
7.			0,7	0,5	0,3	0,31		0,01	0,09
8.			0,8	0,5	0,3	0,32		0,10	0,03
9.			0,9	0,5	0,3	0,33		0,11	0,04
10.			0,7	0,6	0,3	0,34		0,12	0,05
11.			0,8	0,6	0,3	0,35		0,13	0,06
12.			0,9	0,6	0,3	0,36		0,02	0,07
13.			0,8	0,7	0,3	0,37		0,02	0,08
14.			0,9	0,7	0,3	0,38		0,02	0,09
15.			0,9	0,8	0,3	0,39		0,10	0,04
16.			0,6	0,5	0,4	0,40		0,11	0,05
17.			0,7	0,5	0,4	0,41		0,12	0,06
18.			0,8	0,5	0,4	0,42		0,13	0,07
19.			0,9	0,5	0,4	0,43		0,03	0,08
20.			0,7	0,6	0,4	0,44		0,03	0,09
21.			0,8	0,6	0,4	0,45		0,10	0,05
22.			0,9	0,6	0,4	0,46		0,11	0,06
23.			0,8	0,7	0,4	0,47		0,12	0,07
24.			0,9	0,7	0,4	0,48		0,13	0,08
25.			0,9	0,8	0,4	0,49		0,04	0,09
26.			0,7	0,6	0,5	0,51		0,01	0,15
27.			0,8	0,6	0,5	0,52		0,01	0,16
28.			0,9	0,6	0,5	0,53		0,02	0,15
29.			0,8	0,7	0,5	0,54		0,02	0,16
30.			0,9	0,7	0,5	0,55		0,03	0,15

Раздел «Математическая статистика»

1. Составьте логическую схему базы знаний по темам курса и перечень основных зависимостей и формул.

2. Решите самостоятельно следующие задачи. Данные своей задачи возьмите по номеру, соответствующему вашему порядковому номеру.

1. Из таблицы 1 чисел выборки из равномерного распределения на отрезке [0,100] возьмите подряд 100 чисел, начиная с номера 4 N, где N – ваш порядковый номер в списке группы (дойдя до конца таблицы, перейдите в её начало). Возьмите в качестве интервалов группировки интервалы (0,20), (20,40) …. (80,100) и напишите таблицу эмпирического распределения для этих интервалов. По этой таблице постройте гистограмму и полигон, сосчитайте эмпирическое среднее, дисперсию (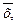 S²), эмпирическое среднеквадратическое отклонение. Выпишите теоретические значение для этих величин и сравните их с эмпирическими.

Таблица 1.

Последовательность случайных чисел,

распределенных равномерно на отрезке [0,100]

2. Из таблицы 2 чисел выборки из нормального распределения N(0,1) возьмите подряд 100 чисел, начиная с номера 4 N, где N – ваш порядковый номер в списке группы (дойдя до конца таблицы, перейдите в её начало). Возьмите в качестве интервалов группировки интервалы (-3,-2), (-2,-1) … (2,3) и напишите таблицу эмпирического распределения для этих интервалов. По этой таблице постройте гистограмму и полигон, сосчитайте эмпирическое среднее, дисперсию (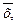 S²), эмпирическое среднеквадратическое отклонение. Выпишите теоретические значение для этих величин и сравните их с эмпирическими.

Таблица 2.

Последовательность случайных чисел,

имеющих распределение N(0,1)

0,414	0,011	0,666	-1,132	-0,410	-1,077	1,484	-0,340	0,789	-0,494
0,364	-1,237	-0,044	-0,111	-0,210	0,931	0,616	-0,377	-0,433	1,048
-0,037	0,759	0,609	-2,043	-2,290	0,404	-0,543	0,486	0,869	0,347
2,816	-0,464	-0,632	-1,614	0,372	-0,074	-0,916	1,314	-0,038	0,673
0,563	-0,107	0,131	-1,808	0,284	0,458	1,307	-1,625	-0,629	-0,504
-0,056	-0,131	0,048	1,879	-1,016	0,360	-0,119	2,331	1,672	-1,053
0,840	0,246	-0,237	-1,312	1,603	-0,952	-0,566	1,600	0,465	1,931
0,110	0,251	0,116	-0,957	-0,190	1,479	-0,986	1,249	1,934	0,070
-1,358	-1,246	-0,959	-1,297	-0,722	0,925	0,783	-0,402	0,619	1,826
1,272	-0,945	0,494	0,050	-1,696	1,876	0,063	0,132	0,682	0,544
-0,417	-0,666	-0,104	-0,253	-2,543	-1,133	1,987	0,668	0,360	1,927
1,183	1,211	1,765	0,035	-0,359	0,193	-1,023	-0,222	-0,616	-0,060
-1,319	-0,785	-0,430	-0,298	0,248	-0,088	-1,379	0,295	-0,115	-0,621
-0,618	0,209	0,979	0,906	-0,096	-1,376	1,047	-0,872	-2,200	-1,384
1,425	-0,812	0,748	-1,095

3. В условиях предыдущей задачи построить 95%-ый доверительный интервал для математического ожидания генеральной совокупности при условии, что дисперсия генерального распределения известна и равна 1.Попало ли оцениваемое значение в доверительный интервал?

4. То же задание, что и в задаче 3, но считать, что дисперсия генерального распределения неизвестна. Попало ли оцениваемое значение в доверительный интервал? Сильно ли различаются интервалы, построенные в 3 и 4 задачах?

5. Производительность стальных канатов долгое время обеспечивал прочность каната на разрыв μ=55000 кг при стандартном отклонении

σ = 500кг. После усовершенствования процесса изготовления, производитель стал утверждать, что прочность каната на разрыв возросла. При испытании выборки из п=50 канатов получено, что средняя выборочная прочность составляет 55250 кг. Заказчик решил проверить гипотезу Н₀: μ=55000 при уровне значимости 0,05 (так как он сомневается в увеличении μ). Пройдет ли эта гипотеза?

Дата добавления: 2014-12-07