Ошибки измерения (погрешности) и причины их возникновения

I. Элементы теории погрешностей

Физические величины связаны между собой определенными закономерностями. Установление количественных законов, показывающих, как меняются одни из измеряемых величин при изменении других, является одной из важнейших задач экспериментальной физики. Поэтому увеличение точности измерений необходимо для более глубокого познания закономерностей материального мира.

Методы измерения физических величин непрерывно совершенствуются. Например, в 1675 году датский ученый Олаф Рёмер впервые нашел значение скорости света: 215000 км/с. Фуко в 1862 году в лабораторных условиях измерил скорость света. У него она получилась равной 296000 км/с. В 1927 году Майкельсон получил для скорости света значение, равное 299796 км/с. Сегодня в физике принято значение скорости света, полученное в 1957 году: (299793 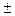0,3) км/с. В случае приближенных расчетов принимают скорость света равной 3 ^. 10⁸ м/с.

Повышения точности измерений позволяет обнаружить, казалось бы, незначительные отступления от физических законов, которые ранее упускались из виду. Такого рода поправки позволяют совершенствовать существующую теорию и учитывать их при выводе новых законов. Например, уравнение состояния идеального газа Менделеева-Клапейрона:

не могло дать хорошего согласия с экспериментом, так как не учитывались собственные размеры молекул и сложный характер их взаимодействия между собой. Более детальное рассмотрение этого вопроса привело к уравнению Ван-дер-Ваальса:

Иногда установленные новые эмпирические соотношения позволяют создавать совершенно новые теории. Например, закономерности, обнаруженные в спектре водорода (работы Бальмера, Ридберга, Ритца), послужили толчком к созданию теории атома водорода и далее квантовой механики (работы Бора, Гейзенберга и др.).

Таким образом, между практикой и теорией существует тесная связь, которая приводит к непрерывному развитию физики, все глубже и точнее отражающей объективные закономерности окружающего нас мира.

Между тем, вследствие неточности измерительных приборов, неполноты наших знаний, трудности учета всех побочных явлений при измерениях неизбежно возникают ошибки (погрешности). Погрешностью измерений называют разность между истинным значением измеряемой величины и результатом измерений. Теория погрешностей указывает на то, как следует вести измерения и их обработку, чтобы при достоверности результатов допущенные ошибки были минимальными.

В процессе выполнения экспериментальных работ, как в учебных, так и в научно-исследовательских лабораториях студенту приходится постоянно измерять и вычислять различные величины; при этом важно иметь представление о том, как правильно оценивать полученный результат, добиться разумной точности, уметь найти и оценить ошибку измерения.

Бессмысленно говорить об абсолютной точности произведенного измерения. Невозможно указать точно, например, размер атома или элементарной частицы, число молекул в комнате или единице ее объема и т. п. Можно говорить лишь о той или иной степени приближенности к искомой величине, о большей или меньшей ошибке или погрешности в произведенном измерении.

В перечисленных примерах нельзя назвать точное число, соответствующее размеру или количеству, потому что эти величины находятся в состоянии непрерывного изменения. Отсюда становится ясным, почему, например, нельзя измерить деталь с точностью до диаметра атома или число молекул в комнате до единиц. Однако диктуемой, как правило, техническими потребностями этой точности и не требуется.

Чем же ограничивается точность измерения, от чего зависит величина допускаемой ошибки и каковы ее источники? Сначала определим понятие ошибки (погрешности) измерения. Под погрешностью измерения D х понимают отклонение результата измерения х от истинного значения х _ист измеряемой величины: D х = х - х _ист. Эта погрешность выражена в единицах измеряемой величины и называется абсолютной погрешностью измерения.

Первой и, к сожалению, достаточно распространенной причиной ошибок служат так называемые промахи. Промахи (грубые погрешности) – это погрешности, значения которых существенно превышают ожидаемые при данных условиях. К ним относятся, например, неверно поставленные часы или неточно установленный нуль прибора, неправильная установка самого прибора (допустим, вертикальная вместо горизонтальной), неправильно записанная цифра или неразборчивая запись в черновике, как следствие, неверно переписанные данные и т. п.. В этом случае результат отдельного измерения резко отличается от результатов других измерений, выполненных при тех же условиях. Избежать этого вида ошибок позволяет серьезная предварительная подготовка и внимательное продуманное проведение эксперимента.

Второй источник трудно контролируемых ошибок связан с методом измерения, конструкцией прибора и влиянием незаметных, на первый взгляд, факторов. Так, изменение длины деревянной линейки в зависимости от влажности воздуха или размера металлических приборов - от температуры, а также спешащий или отстающий секундомер, ослабленная пружина весов, растворение вещества, предназначенного для спектрального анализа, растворителем, содержащим искомое вещество и т. п. Во всех перечисленных случаях допускаемая ошибка характеризуется отклонением в какую–либо одну сторону и называется систематической. Таким образом, систематическая погрешность – это составляющая погрешности измерений, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины.

Для избежания подобного рода ошибок (сведения их к минимуму) необходимо тщательно готовить экспериментальные установки, приборы и оборудование, исключая возможные факторы, влияющие на результат; выбирать методы, позволяющие более точно определять значения величин. Приборы и оборудование должны храниться должным образом и периодически проверяться (сравниваться с эталоном). Минимальная относительная систематическая погрешность определяется классом точности прибора. Классом точности называется максимальная абсолютная погрешность прибора, выраженная в процентах от всей действующей шкалы прибора. По классу точности прибора и пределу измерения определяется абсолютная погрешность. Если измеряемая величина меньше предела измерения прибора, то ее относительная ошибка будет больше класса точности. Абсолютная систематическая погрешность в некоторых случаях определяется как половина цены наименьшего деления шкалы прибора или как половина цены последней значащей цифры (в случае цифрового прибора). В случае равномерной шкалы эта погрешность одинакова для всех измерений.

Третий вид ошибок - случайные ошибки. Они имеют место всегда при любом измерении, вызываются различными причинами и приводят к отклонению результатов, как в большую, так и в меньшую сторону. Другими словами, случайная погрешность измерения – составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях одной и той же величины. Она возникает от многих причин, каждая из которых в отдельности мало влияет на результат измерения. К такого рода ошибкам относятся, например, ошибки, обусловленные различным прижатием микрометрического винта или ножек штангенциркуля, различное положение глаза при отсчете по шкале и т. п. Вся статистическая теория погрешностей связана с изучением и учетом ошибок именно такого рода.

В общем случае при измерении любой величины могут присутствовать все три вида ошибок, но последний вид будет представлен всегда.

Дата добавления: 2014-12-07