Работа с сетями Петри

Сеть Петри определяется как формальная система, характеризуемая 4 формальными объектами: S = < P, T, E, M0 >, где

· P - конечное множество позиций;

· T - конечное множество переходов;

· E - конечное множество дуг;

· M0 - начальная маркировка.

Графически сеть Петри изображается двудольным графом с двумя типами вершин P и T. При переходе от грамматики к сети Петри позиции ассоциируют с нетерминальными символами, а переходы - с терминальными. Позиции могут иметь несколько входящих и исходящих дуг, а переходы - одну входящую дугу и не более одной исходящей дуги для автоматных сетей.

Процедура минимизации конечного автомата с использованием сети Петри:

1. На сети выделяются 2 позиции, имеющие одинаковое количество одинаковых входных переходов.

2. Позиции склеиваются. При этом множества входящих и исходящих дуг этих позиций объединяются без дублирования.

3. На сети выделяются 2 позиции, имеющие одинаковое

количество одинаковых выходных переходов.

4. Позиции склеиваются. При этом множества входящих и

исходящих дуг этих позиций объединяются без дублирования.

5. Если на найденные позиции есть ссылки из других позиций, то они остаются в сети, иначе удаляются после склеивания вместе с входными и выходными дугами и соответствующими переходами.

6. Если из некоторой позиции по одинаковому переходу xi существует более одной выходной позиции, то такие выходные позиции должны быть склеены.

Процедура повторяется с п. 1 до тех пор, пока позиции сети могут быть склеены.

Рассмотрим построение сети Петри для автоматной грамматики. Выполняя все необходимые правила построения сети и минимизации автомата по сети, последовательно получим сети, приведенные на рис.1 -3. На последней сети Петри проставлены ri, по разметке которых легко сравнить результаты минимизации автомата по сети Петри с минимизацией автомата по методике алгоритма Мура (См. табл. 6).

Рис. 1. Сеть Петри, составленная по автоматной грамматике

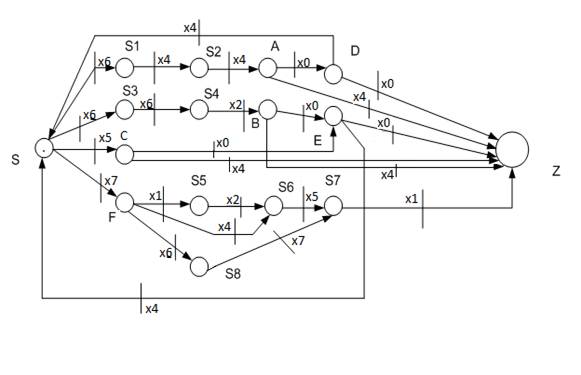
Применяя выше названные правила минимизации сети Петри, можно объединить вершины {D, E} и {A,B,C} согласно правилам 3-4. У них имеется на выходе одинаковое количество одинаковых переходов. Затем объединяются вершины {S1,S3} согласно правилам 1-2. Построим сеть после преобразования, получим:

Рис. 2. Минимизированная сеть Петри

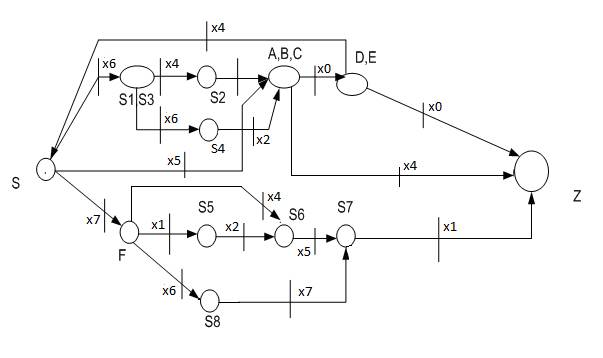
Если провести параллель между состояниями минимизированного детерминированного автомата и минимальной сетью Петри, то можно установить соответствие:

r0	r1	r2	r3	r4	r5	r6	r7	r8	r9	r10	r11
S	A,B,C	D,E	F	S1,S3	S2	S4	S5	S6	S7	S8	Z

Дата добавления: 2014-12-07