Кодирование состояний автомата

Кодирование автомата определяет обеспечение одного из важнейших свойств автомата, а именно устойчивость автомата по отношению к состязаниям элементов памяти. Переходам автомата из одного состояния в другое сопоставим изменение состояний элементов памяти.

Если на входы двух элементов памяти подать одновременно один сигнал, то на выходе сигнал возникнет не одновременно. Это явление называется состязаниями элементов памяти.

Считается, что автомат работает устойчиво, если в процессе его работы не возникает критических состязаний. Критическим считаем такое состязание элементов памяти, когда автомат под действием одного и того же входного воздействия может перейти в разные состояния. Поэтому первоочередной задачей кодирования является обеспечение устойчивости автомата.

Существует 2 способа кодирования автомата. Первый характеризуется устранением всех состязаний элементов памяти. Для этого всем внутренним

состояниям, для которых существуют переходы, приписываются соседние кодовые комбинации, отличающиеся друг от друга одной переменной.

Второй способ кодирования связан только с устранением критических состязаний. Методы первой и второй групп имеют свои преимущества и свои недостатки.

Чтобы приступить к кодированию, которое необходимо выполнить для построения в последующем структурной схемы автомата, введем в табл. 6 переходов автомата символ конца цепочки входных символов, например, символ x3, который оказался неиспользуемым в рассматриваемой грамматике. Соответственно, необходимо в таблицу переходов ввести переход из заключительного состояния r11 в начальное состояние r0 по входному символу x3. Новая таблица переходов примет вид, показанный табл. 7, в которой последний столбец отведен для формируемых кодов состояний автомата.

Число внутренних переменных кода, изменяющих свои значения при переходе автомата из одного состояния в другое, есть расстояние по Хеммингу между этими кодами.

Наименьшее число переменных, необходимое для кодирования синхронного автомата с N внутренними состояниями определяется формулой:

n = ] log2 (N) [

] [ - ближайшее сверху к log₂ (N) целое число. Например, при N=13 n

будет равно 4.

Число кодовых переменных, необходимое для кодировки состояния автомата соседними кодами определяется по формуле:

n = 2 · ] log2 (N) [ - 1.

Знаком · обозначена операция умножения.

Чем меньше внутренних переменных изменяется при любом переходе, тем проще реализация функций переходов, т.е. проще структурная реализация автомата.

В курсовой работе используется код минимальной длины. В связи с этим может возникнуть ситуация, когда все соседние коды заняты, а состояния автомата еще не закодированы в полном объеме. Это требует увеличения расстояния по Хеммингу на следующем шаге кодирования. Кодирование будем осуществлять методом проб и ошибок.

Таблица 7

	x0	x1	x2	x3	x4	x5	x6	x7	Код
r0 нач. сост.					r11	r1	r4	r3
r1	r2				r11
r2	r11				r0
r3		r7			r8		r10
r4					r5		r6
r5					r1
r6			r1
r7			r8
r8						r9
r9		r11
r10								r9
r11 закл. сост.				r0

Таблица 8

	x0	x1	x2	x3	x4	x5	x6	x7	Код
r0 нач. сост.					r11	r1	r4	r3
r1	r2				r11
r2	r11				r0
r3		r7			r8		r10
r4					r5		r6
r5					r1
r6			r1
r7			r8
r8						r9
r9		r11
r10								r9
r11 закл. сост.				r0

Таблица 9

	x0	x1	x2	x3	x4	x5	x6	x7	Код
r0 нач. сост.					r11	r1	r4	r3
r1	r2				r11
r2	r11				r0
r3		r7			r8		r10
r4					r5		r6
r5					r1
r6			r1
r7			r8
r8						r9
r9		r11
r10								r9
r11 закл. сост.				r0

При этом используем направления кодирования состояний, представленные на рис. 4.

r10 r3 r0 r11

r8 r7 r4 r1 r2

r9 r5 r6

Рис. 4

Выполним три варианта кодирования (Таблицы 7, 8, 9), из которых выберем наилучший на основе критерия Махалонобиса. Критерием кодирования автомата считаем минимум функционала Махаланобиса.

,

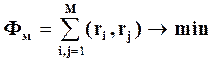где M - число переходов. Через (r_i, r_j) обозначено расстояние между кодами r_i и r_j по Хеммингу.

В результате получим, что в первом случае суммарное расстояние по Хеммингу для 20 переходов равно 32, а во втором и третьем случае - 26. Выберем третий вариант.

Дата добавления: 2014-12-07