
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод скользящих средних в матричной форме
|
|
|
|
2.
1.
Алгоритмический подход к выделению тренда
1. Метод скользящих средних. Способ медианного сглаживания.
2. Взвешенная скользящая средняя (вывод весовых коэффициентов при сглаживании ряда по полиномам).
3. Краевые эффекты, метод восстановления недостающих уровней.
4. Влияние процедуры выделения тренда методом скользящих средних на остальные компоненты

Существенным в понятии тренда является гладкость, что на практике означает желательность его представления непрерывной и дифференцируемой функцией времени.
При анализе рядов динамики возникает важная задача: определение основной тенденции в развитии исследуемого явления. В некоторых случаях общая тенденция ясно прослеживается в динамике показателя, в других ситуациях она может не просматриваться из-за ощутимых случайных колебаний.
На практике для обнаружения общей тенденции часто используют простой прием – укрупнение интервалов. Например, ряд недельных данных можно преобразовать в ряд месячной динамики, ряд квартальных данных заменить годовыми уровнями. Уровни нового ряда могут быть получены суммированием уровней исходного ряда либо могут представлять средние значения.
Распространенным приемом при выявлении тенденции развития является сглаживание временного ряда. Суть различных приемов сглаживания сводится к замене фактических уровней временного ряда расчетными, обладающими меньшей колеблемостью. Это способствует более четкому проявлению тенденции развития. Иногда сглаживание применяют как предварительный этап перед использованием других методов выделения тенденции.
Скользящие средние позволяют сгладить как случайные, так и периодические колебания, выявить имеющуюся тенденцию в развитии процесса, и поэтому, являются важным инструментом при фильтрации компонент временного ряда.
Алгоритм сглаживания по простой скользящей средней может быть представлен в виде следующей последовательности шагов:
1. Определяют длину интервала сглаживания  , включающего в себя
, включающего в себя  последовательных уровней ряда
последовательных уровней ряда  . При этом надо иметь в виду, что чем шире интервал сглаживания, тем в большей степени взаимопогашаются колебания, и тенденция развития носит более плавный характер. Чем выше колеблемость, тем шире должен быть интервал сглаживания.
. При этом надо иметь в виду, что чем шире интервал сглаживания, тем в большей степени взаимопогашаются колебания, и тенденция развития носит более плавный характер. Чем выше колеблемость, тем шире должен быть интервал сглаживания.
2. Разбивают весь период наблюдений на участки, при этом интервал сглаживания как бы скользит по ряду с шагом, равным 1.
3. Рассчитывают арифметические средние из уровней ряда, образующих каждый участок.
4. Заменяют фактические значения ряда, стоящие в центре каждого участка, на соответствующие средние значения.
При этом удобно брать длину интервала сглаживания  в виде нечетного числа:
в виде нечетного числа: 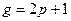 , так как в этом случае полученные значения скользящей средней приходятся на средний член интервала.
, так как в этом случае полученные значения скользящей средней приходятся на средний член интервала.
Наблюдения, которые берутся для расчета среднего значения, называют активным участком сглаживания.
При нечетном значении  все уровни активного участка могут быть представлены в виде:
все уровни активного участка могут быть представлены в виде:
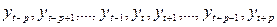 , а скользящая средняя определена по формуле:
, а скользящая средняя определена по формуле:
 ,
,
где  - фактическое значение
- фактическое значение  -го уровня;
-го уровня;
 - значение скользящей средней в момент времени
- значение скользящей средней в момент времени  ;
;
 - длина интервала сглаживания.
- длина интервала сглаживания.
Процедура сглаживания приводит к полному устранению периодических колебаний во временном ряду, если длина интервала сглаживания берется равной или кратной циклу, периоду колебаний.
Для устранения сезонных колебаний желательно было бы использовать четырех- и двенадцатичленную скользящие средние, но при этом не будет выполнятся условие нечетности длины интервала сглаживания. Поэтому при четном числе уровней принято первое и последнее наблюдение на активном участке брать с половинными весами:
 .
.
При использовании скользящей средней с длиной активного участка 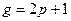 - первые и последние
- первые и последние  уровней ряда сгладить нельзя, их значения теряются.
уровней ряда сгладить нельзя, их значения теряются.
Метод простой скользящей средней применим, если графическое изображение временного ряда напоминает прямую. Если для процесса характерно нелинейное развитие, то простая скользящая средняя может привести к существенным искажениям. В этих случаях более надежным является использование взвешенной скользящей средней.
Кроме использования среднего арифметического возможно также другая модификация – использование медианы. Основное достоинство медианного сглаживания – устойчивость к выбросам. В основе лежит вычисление скользящей медианы.
Способ медианного сглаживания предполагает следующую последовательность шагов:
¾ Определяют длину интервала сглаживания  , включающего в себя
, включающего в себя  последовательных уровней ряда
последовательных уровней ряда  .
.
¾ Ранжирование (упорядочивание по возрастании.) выбранного отрезка ряда.
¾ определение медианы (центрального члена) ранжированного отрезка временного ряда.
¾ Замена фактического значения ряда, стоящего в центре каждого участка, на медианное значение.
¾ сдвиг на одно значение...
Поскольку любая гладкая функция при самых общих допущениях может быть локально представлена полиномом с довольно высокой степенью точности, предпочтительной является следующая процедура. Подбираем полином к первой группе, скажем, из 2р+1 членов ряда (далее будет ясно, почему берется нечетное число) и используем полином для определения значения тренда в (р+1), средней точке группы. Затем подбираем полином того же порядка к группе, состоящей из второго, третьего,..., (2р+2)-го наблюдения, и находим значение тренда в (р+2)-ой точке и так далее тем же способом вдоль всего ряда до последней группы из (2р+1) членов. В действительности нет необходимости подбирать полиномы каждый раз. Покажем, что эта процедура эквивалентна линейной комбинации наблюдений с коэффициентами, которые могут быть определены раз и навсегда.
Предположим, например, что мы хотим подбирать полином третьего порядка к группам по семь точек. Без потери общности примем, что рассматриваются моменты времени t=-3, -2, -1, 0, 1, 2, 3. Запишем искомый полином:
уt=a0+a1t+a2t2+a3t3
Коэффициенты а определяются методом наименьших квадратов (МНК), то есть:

Дифференцирование по а дает четыре уравнения такого типа:
 (*)
(*)
Суммы нечетных порядков t от -3 до +3 равны 0, и уравнения сводятся к виду
 (1)
(1)
Пока нас интересует только a0, значение ряда в момент t=0. Используя лишь первое и третье из уравнений системы (1), получаем
 =
=  =
=

Следовательно, значение тренда в какой-либо точке равно средневзвешенному значению семи точек с данной точкой в качестве центральной и весами
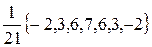 , которые в силу симметрии можно записать короче:
, которые в силу симметрии можно записать короче:

По вполне понятным причинам это значение называется скользящим средним.
Эта процедура имеет самый общий характер. Если к (2р+1) точкам подбирают полином порядка к, необходимо минимизировать

Минимизация приводит к уравнениям (1), аналогичным рассмотренным ранее, которые разбиваются на две подсистемы (одна содержит коэффициенты с четными индексами, другая с нечетными). Решение относительно a0 зависит от численных значений суммы  и линейных функций от у типа
и линейных функций от у типа 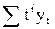 . Далее, значением тренда в точке, t= l будет взвешенное среднее значений от yl-m до yl+m. Приведем веса для подсчета скользящего среднего подбором полиномов до пятого порядка к отрезкам ряда длиной до 13 точки (таблица Каудена):
. Далее, значением тренда в точке, t= l будет взвешенное среднее значений от yl-m до yl+m. Приведем веса для подсчета скользящего среднего подбором полиномов до пятого порядка к отрезкам ряда длиной до 13 точки (таблица Каудена):
Полиномы второго и третьего порядка
| Длина интервала сглаживания | Весовые коэффициенты |
| [-3,+12,+17]*1/35 | |
| [-2,+3,+6,+7]*1/21 | |
| [-21,+14,+39,+54,+59]*1/231 | |
| [-36,+9,+44,+69,+84,+89]*1/429 | |
| [-11,0,+9,+16,+21,+24,+25]*1/143 |
Полиномы четвертого и пятого порядка
| Длина интервала сглаживания | Весовые коэффициенты |
| [5,-30,+75,+131]*1/231 | |
| [15,-55,+30,+135,+179]*1/429 | |
| [18,-45,-10,+60,+120,+143]*1/429 | |
| [110,-198,-135,+110,+390,+600,+677]*1/2431 |
Введем следующие обозначения:
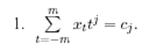
Т.к. xt и tj известны, то cj также известно для каждого j = 0, 1 ,..., p.

3. Обозначим через  величину:
величину:

Тогда:

а система (*) принимает вид:

В краткой записи эта система выглядит как:

где  — известна (кроме того, элементы с нечетными индексами равны
— известна (кроме того, элементы с нечетными индексами равны
нулю) и вектор c также известен.
Из полученной системы следует:

Если переобозначить c / 2 = b, то система примет вид:

Теперь можно использовать формулу Крамера для нахождения ak:

где M k +1 получается из матрицы  заменой (k + 1) -го столбца вектором
заменой (k + 1) -го столбца вектором
b.
Таким образом:

Рассмотрим частный случай, когда m = 2 и p = 2, т.е. временной ряд аппроксимируется полиномом второй степени:

Система уравнений, которую нужно решить относительно ak (k = 0, 1, 2) имеет
вид:


Для нахождения определителя раскладываем по второй строке:

Отсюда

и получается как взвешенная средняя из уровней временного ряда, входящих в отрезок. Оценки параметров a 1, a 2, ..., ap необходимы для вычисления значений тренда в первых m и последних m точках временного ряда, поскольку рассмотренный способ сглаживания ряда через a 0 сделать это не позволяет. Размерность матрицы  определяется степенью полинома: (p +1) * (p +1), пределы суммирования во всех формулах задаются длиной отрезка скольжения. Следовательно, для выбранных значений p и m можно получить общее решение в виде вектора (a 0, a 1 ,..., ap) /.
определяется степенью полинома: (p +1) * (p +1), пределы суммирования во всех формулах задаются длиной отрезка скольжения. Следовательно, для выбранных значений p и m можно получить общее решение в виде вектора (a 0, a 1 ,..., ap) /.
Легко вывести некоторые свойства таких скользящих средних:
¾ сумма весов равна единице.
¾ веса симметричны относительно серединного значения;
¾ в силу второго свойства значения тренда не зависят от направления отсчета времени;
¾ поскольку определяющие уравнения разделяются на две подсистемы, значение a0 будет тем самым независимо от того, присутствует член а3t3 или нет. Другими словами, для полиномов четного порядка 2l формулы будут те же самые, что и для полиномов порядка 2l+1.
¾ формулы не позволяют вычислить значения тренда для первых и последних m значений ряда.
Можно вывести формулы для построения трендов на четном числе точек, однако при этом были бы получены значения трендов в серединах временных интервалов между наблюдениями, что, очевидно, весьма неудобно.
Иногда более удобно записывать эти формулы на языке разностей рядов, особенно когда разности меньше, чем исходные значения ряда. Запишем разность (вперед) как:

так что  и т.д. получаем, например,
и т.д. получаем, например,

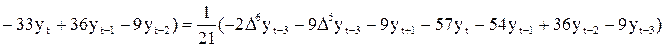 =
=  (2)
(2)
это является выражением того факта, что построенная линия тренда пройдет точно через значения ряда, если они отражают кубическую зависимость, так как разности четвертого и более высоких порядков тогда равны нулю. Уравнение (2) имеет также преимущество, которое заключается в том, что в нем в явном виде представлена разность между рядом и трендом.
Скользящее среднее можно также рассматривать как среднее разностей. Например, легко проверить, что


Приведем веса:
Второй и третий порядки
| Длина интервала сглаживания | Весовые коэффициенты |

| |

| |

| |

| |

|
четвертый и пятый порядки
| Длина интервала сглаживания | Весовые коэффициенты |

| |

| |
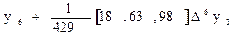
| |

|
При применении данных весовых коэффициентов обычно рассчитывают дисперсию.
Если применить веса к случайному ряду с дисперсией  , то результирующий ряд будет (например
, то результирующий ряд будет (например 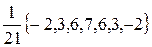 ):
):

Таким образом применение весов минимизирует сумму квадратов остатков, уменьшает дисперсию до одной трети. Коэффициент при  , характеризующий дисперсию скользящего среднего, обычно называют степенью уменьшения(увеличения) ошибки.
, характеризующий дисперсию скользящего среднего, обычно называют степенью уменьшения(увеличения) ошибки.
Довольно громоздкие числа, встречающиеся в этих формулах, хотя и не создают вычислительных трудностей, но возможны способы упрощения.
Один из способов упрощения заключается в сведении вычисления скользящего среднего к итеративной обработке простых средних, то есть таких, для подсчета которых используются равные веса. Операции умножения здесь в основном сводятся к суммированию. Например, если взять простое скользящее среднее трех членов и затем построить другое скользящее среднее пяти скользящих членов первого типа, то со множителем 1/15 получим веса:
1, 1, 1
1, 1, 1
1, 1, 1
1, 1, 1
1, 1, 1
[1, 2, 3, 3, 3, 2, 1]
Самый короткий, но несколько более сложный метод выведения формул основан на итеративной обработке простых средних следующим образом.
Если вторую «центральную» разность определить как
 (1), то можно показать, что для простого скользящего среднего m членов
(1), то можно показать, что для простого скользящего среднего m членов  , справедливо равенство:
, справедливо равенство:
 и т.д. (2)
и т.д. (2)
Если например, требуется представить ряд кубическим полиномом, так что четвертые разности равны нулю, то получим точную формулу:
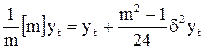 (3)
(3)
Пример: Формула Спенсера для 15 точек. (Формула скользящего среднего Спенсера, по имени актуария, который вывел ее в 1904 г.)
Рассмотрим три последовательных усреднения по 4, по 4 и по 5 членам с равными весами. С точностью до разностей третьего порядка согласно (3) имеем

Естественным образом возникает вопрос, какой степени полином следует выбирать и какой должна быть длина отрезка скольжения. Закономерность такова: чем выше степень полинома и короче отрезок скольжения, тем ближе расчетные значения к первоначальным данным. При этом, помимо тенденции могут воспроизводиться и случайные колебания, нарушающие ее смысл. И наоборот, чем ниже степень полинома и чем длиннее отрезок скольжения, тем более гладкой является сглаживающая кривая, тем в большей мере она отвечает свойствам тенденции, хотя ошибка аппроксимации будет при этом выше.
В принципе, если ставится задача выявления тренда, то, с учетом особенностей покомпонентного разложения временного ряда, следует ориентироваться не на минимальную остаточную дисперсию, а на стационарность остатков, получающихся после исключения тренда.
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 2269; Нарушение авторских прав?; Мы поможем в написании вашей работы!