Выравнивание шейного сегмента позвоночника 1 страница

Пример

Дана матрица решений 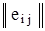, размером 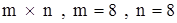, результатами которой есть убытки. Осуществить выбор наилучшего варианта решения с помощью критериев: минимаксного, Байєса-Лапласа и Сэвиджа. Известно, что вероятности появления внешних состояний 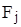, j=1,...,8 имеют следующие значения: .

.

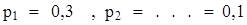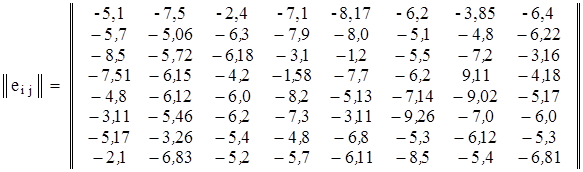Решение. Сначала будем искать оптимальный вариант решения с помощью ММ-критерия, для этого матрицу решений дополняем столбцом 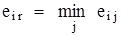- наименьших результатов каждой строки, то есть

.

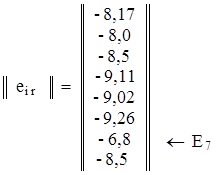Теперь будем выбирать варианты 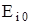, в строках которых стоит наибольшее значение 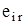этого столбца, то есть 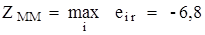. Этот результат отвечает оптимальному варианту .

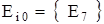Применим критерий Байєса-Лапласа для поиска оптимального варианта. Найдем математические ожидания каждой строки 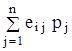и запишем их в дополнительный столбец :

=

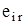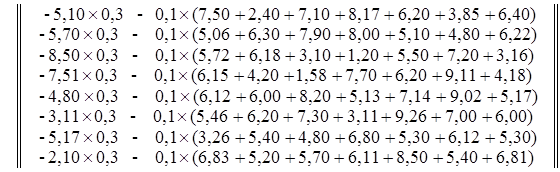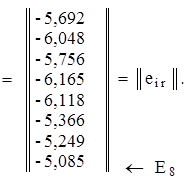
Далее применим оценочную функцию (8) и найдем оптимальный вариант. Поскольку 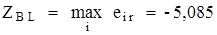, то такой результат отвечает оптимальному варианту .

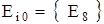Для использования критерия Сэвиджа построим матрицу разностей 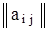в соответствии с формулой (9)

.

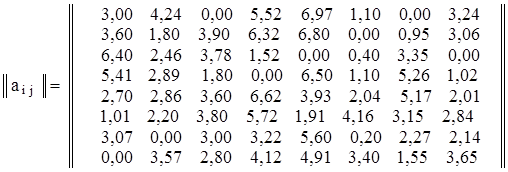Для этой матрицы построим дополнительный столбец соответственно формуле (10) и с помощью оценивающей функции 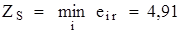найдем оптимальный вариант решения .

.

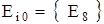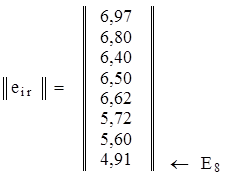Таким образом, используя классические критерии, мы получили ряд оптимальных вариантов . Для выбора наилучшего из них необходимы дополнительные условия.

Порядок выполнения работы.

Дана матрица решений, размером 8´8 результатами которой есть или прибыль или убытки осуществить выбор оптимального варианта решения с помощью критериев:

1. Минимаксного;

2. Байєса-Лапласа;

3. Сэвиджа.

Матрица решений и распределение вероятностей появления внешних состояний выбираются по номеру в списке группы.

Варианты матрицы решений находятся в таблице 1. Распределение вероятностей 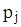- появления внешних состояний 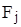, j=1,...,n подчиняется значением, которые указаны в таблицы 2 по вариантам.

Табл. 1. Варианты матрицы решений:

Вариант 1			Вариант 2
										-8	-53	-53	-33	-91	-89	-51	-34
										-97	-75	-37	-16	-63	-77	-28	-28
										-94	-90	-97	-19	-93	-75	-84	-85
										-35	-35	-31	-37	-78	-95	-93	-34
										-3	-11	-3	-59	-38	-81	-62	-42
										-4	-96	-76	-1	-37	-67	-78	-75
										-16	-73	-21	-70	-82	-75	-7	-91
										-27	-16	-19	-87	-55	-79	-31	-85
Вариант 3			Вариант 4
										-78	-60	-44	-74	-66	-79	-72	-91
										-71	-42	-14	-12	-76	-70	-27	-53
										-6	-57	-56	-69	-71	-45	-88	-17
										-70	-95	-74	-3	-79	-90	-47	-63
										-98	-2	-1	-26	-77	-20	-52	-90
										-41	-17	-86	-90	-29	-20	-32	-83
										-14	-33	-24	-32	-30	-62	-11	-5
										-59	-67	-57	-19	-8	-50	-8	-58
Вариант 5			Вариант 6
										-47	-98	-44	-15	-4	-92	-80	-39
										-94	-25	-3	-74	-27	-3	-84	-85
										-75	-50	-2	-13	-45	-57	-42	-40
										-31	-78	-88	-40	-63	-37	-22	-74
										-24	-97	-64	-5	-55	-23	-22	-43
										-6	-22	-5	-2	-32	-72	-67	-72
										-87	-60	-92	-3	-44	-5	-61	-48
										-53	-68	-53	-26	-91	-44	-57	-54

Вариант 7			Вариант 8
										-8	-24	-4	-39	-2	-36	-72	-20
										-85	-61	-15	-85	-57	-38	-9	-3
										-10	-74	-11	-13	-71	-20	-26	-58
										-43	-47	-53	-47	-82	-58	-89	-50
										-15	-11	-67	-65	-3	-62	-72	-95
										-65	-54	-72	-92	-87	-84	-23	-4
										-85	-81	-95	-49	-70	-47	-7	-11
										-16	-78	-76	-63	-27	-13	-17	-46
Вариант 9			Вариант 10
										-6	-84	-38	-9	-75	-68	-47	-57
										-11	-13	-47	-87	-4	-13	-41	-11
										-19	-82	-17	-46	-46	-3	-54	-98
										-1	-40	-24	-18	-45	-73	-36	-62
										-67	-45	-28	-5	-85	-55	-32	-71
										-8	-69	-43	-75	-36	-43	-87	-30
										-57	-52	-83	-73	-89	-1	-57	-30
										-79	-85	-43	-63	-47	-96	-54	-65
Вариант 11			Вариант 12
										-52	-49	-23	-50	-79	-54	-66	-7
										-83	-90	-47	-17	-1	-68	-19	-59
										-36	-3	-29	-3	-71	-86	-86	-5
										-56	-47	-65	-43	-29	-62	-65	-79
										-73	-83	-54	-64	-39	-70	-43	-41
										-57	-90	-44	-59	-31	-65	-25	-65
										-75	-90	-69	-70	-18	-73	-6	-70
										-9	-11	-44	-21	-63	-72	-69	-74

Вариант 13			Вариант 14
										-36	-22	-64	-85	-45	-84	-16	-72
										-11	-73	-9	-37	-39	-73	-44	-56
										-6	-20	-54	-51	-49	-68	-11	-14
										-92	-61	-93	-62	-17	-89	-74	-69
										-48	-29	-82	-74	-79	-21	-7	-19
										-8	-39	-16	-59	-23	-47	-54	-24
										-60	-51	-17	-16	-11	-95	-25	-24
										-64	-79	-29	-9	-96	-39	-36	-17
Вариант 15			Вариант 16
										-80	-76	-87	-33	-7	-43	-18	-7
										-82	-79	-1	-67	-38	-26	-59	-29
										-18	-46	-49	-89	-92	-30	-19	-44
										-63	-53	-20	-90	-24	-48	-75	-13
										-32	-29	-75	-14	-57	-37	-39	-54
										-52	-2	-40	-89	-12	-77	-73	-26
										-20	-88	-46	-23	-73	-96	-54	-55
										-48	-5	-13	-71	-84	-10	-12	-2
Вариант 17			Вариант 18
										-43	-44	-54	-84	-48	-51	-59	-29
										-11	-23	-94	-44	-84	-65	-86	-49
										-85	-89	-60	-51	-32	-40	-79	-21
										-48	-89	-21	-73	-52	-87	-67	-7
										-23	-43	-32	-5	-40	-67	-49	-6
										-78	-38	-12	-1	-54	-21	-32	-68
										-86	-92	-40	-97	-65	-73	-31	-18
										-49	-46	-76	-1	-16	-75	-39	-38

Вариант 19			Вариант 20
										-63	-25	-53	-51	-5	-7	-67	-28
										-29	-50	-88	-80	-95	-24	-81	-44
										-49	-6	-50	-8	-50	-40	-8	-27
										-91	-60	-46	-70	-65	-7	-69	-7
										-56	-49	-3	-14	-9	-46	-36	-67
										-45	-21	-69	-95	-98	-95	-15	-97
										-31	-44	-64	-9	-51	-25	-34	-4
										-70	-9	-50	-95	-9	-58	-26	-67
Вариант 21			Вариант 22
										-10	-91	-14	-62	-10	-68	-93	-16
										-61	-70	-28	-91	-26	-1	-81	-5
										-11	-58	-6	-25	-44	-39	-50	-89
										-71	-4	-79	-42	-66	-34	-78	-30
										-32	-78	-89	-29	-48	-1	-47	-23
										-81	-22	-29	-76	-86	-3	-93	-67
										-24	-13	-23	-26	-63	-10	-96	-77
										-23	-97	-41	-3	-51	-81	-94	-90
Вариант 23			Вариант 24
										-7	-14	-27	-8	-12	-20	-31	-93
										-82	-94	-64	-79	-80	-15	-33	-18
										-41	-80	-84	-25	-86	-7	-19	-61
										-47	-61	-34	-85	-55	-95	-23	-68
										-13	-88	-50	-56	-7	-82	-2	-64
										-80	-6	-27	-73	-4	-27	-46	-6
										-78	-89	-77	-36	-82	-40	-27	-40
										-62	-15	-6	-39	-15	-66	-62	-61

Дата добавления: 2014-12-07