Случайные величины и их вероятностные характеристики

Или

Или

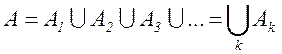
где 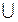- символ объединения событий (логическая операция ИЛИ).

Из определения суммы событий непосредственно вытекают следующие соотношения:

А + А = А, А + U = U, A + V = A, A + B = B + A,

(A + B) + C = A + (B + C).

Произведением (или пересечением, или совмещением) событий А₁, А₂, А₃, … называется такое событие А, которое происходит тогда и только тогда, когда происходят все события вместе («одновременно »). Для обозначения произведения событий применяются следующие записи:

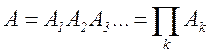
где ∩ - символ пересечения событий (логическая операция И).

Для произведения событий справедливы соотношения:

АА = А, AV = V, AU = A, AB = BA, (AB)C = A(BC)

Понятия суммы и произведения употребляются здесь не в арифметическом смысле, а обозначают соответствующие логические операции.

В основе косвенных методов оценки вероятности сложного события А через вероятности более простых событий А₁, А₂, …А_n базируется на использовании основных теорем теории вероятностей (теорем сложения и умножения вероятностей и их следствий).

Согласно теореме сложения вероятностей вероятность суммы двух событий равна сумме вероятностей этих событий минус вероятность их произведения:

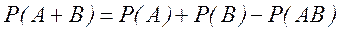(2.3)

Если события А и В несовместимы, то:

(2.4)

Формулы (2.3) и (2.4) обобщаются на сумму любого числа n событий:

(2.5)

(2.6)

Сумма вероятностей несовместимых событий, составляющих полную группу, равна единице:

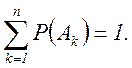(2.7)

Сумма вероятностей двух противоположных событий равна единице:

(2.8)

По теореме умножения вероятностей для двух событий вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что произошло первое:

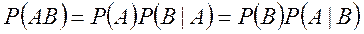(2.9)

где P (A|B) -условная вероятность события А, т.е. вероятность события А, вычисленная в предположении, что имело место событие В.

Если событие А статически не зависит от события В, то P (A|B) = P(A), причем события А и В называются независимыми. При независимых событиях А и В выражение (2.9) принимает вид:

(2.10)

Формулы (2.9.) и (2.10.) обобщаются на n событий А₁, А₂, …А_n:

(2.9а)

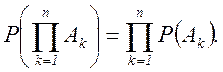(2.10а)

Решение многих практических задач требует совместного использования теорем сложения и умножения вероятностей. В частности, с помощью этих теорем производится расчет вероятности безотказной работы, например, радиотехнических систем.

Из формулы (2.9.) получаем:

(2.11)

Решение многих практических задач требует совместного использования теорем сложения и умножения вероятностей в частности с помощью этих теорем производится расчет вероятностей безотказной работы, например систем передачи информации.

Найдем вероятность Р_n,_k того, что при n независимых испытаниях, исходом которых может быть одно из двух противоположных событий А или Ā, событие А произойдет ровно k раз.

Вероятность события А обозначим Р(А) = Р, тогда Р(Ā) = 1 – Р. Вероятность конкретной комбинации исходов n независимых испытаний, когда при определенных k испытаниях появилось событие А, а при остальных n – k испытаниях – событие Ā, в соответствии с теоремой умножения вероятностей равна P^k (1 – P)^{n – k}, независимо от того, в каком порядке чередовалисьв данной комбинации исходы событий А и Ā. Интересующее нас сложное событие представляет сумму всех исходов n-кратных испытаний, дающих k появлений события А. Поскольку исходы с разным порядком чередования событий А и Ā несовместны, а число исходов, дающих в разной последовательности k появлений события А в n испытаниях, равно числу сочетаний из n элементов по k, то в соответствии с теоремой сложения вероятностей

(2.12)

(При решении многих задач целесообразно использовать «комбинаторные» способы, т.е. теорию Соединений (размещений, перестановок, сочетаний). В формуле (2.12)

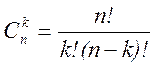– число сочетаний из n элементов по k. Формула (2.12) носит название биноминального закона.

Во многих реальных ситуациях то или иное событие А может появляться лишь как случайное следствие одного из несовместных событий H_i (i= 1, 2, …, n), которые входят в некоторую полную группу событий и называются гипотезами. В таких случаях безусловная вероятность P (A) события A при известных вероятностях гипотез P (H_i) и условных вероятностях P (A|H_i) определяется по формуле полной (или средней) вероятности:

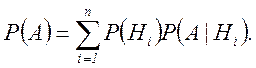(2.13)

При этих же данных, т.е. известных вероятностях P (H_i) и P (A|H_i), можно найти изменение вероятностей гипотез H_i, если предположить, что событие A уже произошло. Задачи подобного типа решаются с помощью теоремы гипотез (или формулы Байеса):

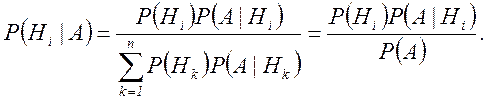(2.14)

Вероятность P (H_i) называется априорной (доопытной), а P (A|H_i) – апостериорной (послеопытной), обратной вероятностью, или функцией правдоподобия той или иной гипотезы об исходе непосредственно не наблюдаемого явления H при известном исходе явления A, если только известны значения вероятностей P (H_j) исходов H_j (в сочетании с любым из исходов А_i) и значения условных вероятностей P (A_i|H_j).

Если случайная величина ξ может принимать конечное число дискретных значений x_i, исчерпывающей вероятностной характеристикой ее служит распределение вероятностей этих значений P_i. (По аналогии со случайными функциями случайные величины обозначим буквами греческого алфавита, а их конкретные реализации – буквами латинского алфавита.)

Если случайная величина ξ непрерывна и может принимать любое значение на интервале [x_min, x_max], то ее статистической характеристикой может служить так называемый интегральный закон распределения F (x)=P(ξ<x), определяющий вероятность того, что случайная величина ξ не превзойдет значение x. Из определения интегрального закона распределения вытекает следующее очевидное соотношение:

где – вероятность того, что случайная величина ξ не выйдет за пределы интервала [x₁, x₂].

Очевидны следующие свойства функции F(x): F(x) – монотонная неубывающая функция;

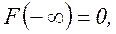
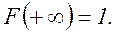
Если функция F(x) дифференцируемая, то в качестве вероятностной характеристики случайной величины удобно использовать дифференциальный закон распределения или закон распределения плотности вероятности

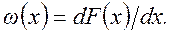(2.15)

Очевидны следующие соотношения:

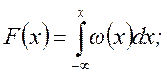
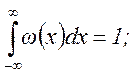
Помимо законов распределения, часто используются числовые характеристики случайных величин, так называемые моменты распределения. Моменты, характеризующие распределение случайных величин относительно нуля, называются начальными.

Для непрерывных случайных величин начальный момент k-го порядка определяется по формуле

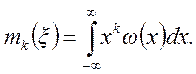(2.16)

Для дискретной случайной величины ξ, принимающей значения x₁, x₂, …, x_n с вероятностями P₁, P₂, …, P_n,

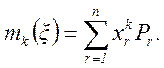(2.17)

Наиболее важное значение имеют моменты 1-го и 2-го порядков. Начальный момент 1-го порядка дает математическое ожидание или среднее значение случайной величины ξ:

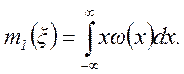(2.18)

Разность Δ_ξ=ξ – m₁(ξ) называется отклонением случайной величины. Моменты распределения отклонений случайной величины называются центральными и обозначаются M_k(ξ). Нетрудно убедиться, что M₁(ξ)=0.

Случайные величины с нулевым средним значением называются центрированными. Любые случайные величины можно свести к центрированным, если перейти к отклонениям Δ_ξ.

Начальный момент 2-го порядка определяет средний квадрат случайной величины ξ:

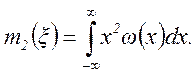(2.19)

Центральный момент 2-го порядка называется дисперсией случайной величины:

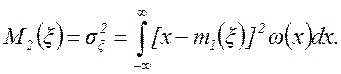(2.20)

Отношение Δ_ξ/σ_ξ называется нормированным отклонением случайной величины.

Центральный и начальный момент 2-го порядка случайной величины связаны простым соотношением:

(2.21)

Для совокупности двух случайных величин ξ₁ и ξ₂ исчерпывающей вероятностной характеристикой служит двумерный интегральный закон распределения F(x₁, x₂)=P(ξ₁<x₁, ξ₂<x₂), определяющий вероятность того, что случайные величины ξ₁ и ξ₂ не превосходят соответственно значений x₁ и x₂. Если функция F(x₁, x₂) дифференцируемая, то вероятностной характеристикой двумерной случайной величины может служить двумерный дифференциальный закон распределения или двумерная плотность вероятностей ω₂(x₁, x₂)=∂²F(x₁, x₂)/∂x₁∂x₂. Аналогично могут быть введены многомерный интегральный закон распределения и многомерные функции распределения для совокупностей из любого числа случайных величин.

Можно также ввести числовые характеристики для совокупности двух случайных величин ξ₁ и ξ₂, имеющих двумерную плотность вероятностей ω₂(x₁, x₂). Весьма важной числовой характеристикой совокупности двух случайных величин является смешанный второй центральный момент или ковариация случайных величин ξ₁ и ξ₂:

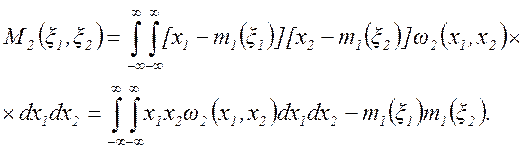(2.22)

Если случайные величины ξ₁ и ξ₂ независимы, то ω₂(x₁, x₂)=ω(x₁)ω(x₂), и двукратный интеграл в (2.22) распадается на произведения двух однократных интегралов:

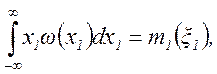
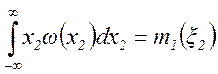
и, следовательно, M₂(ξ₁, ξ₂)=0. Поэтому ковариация M₂(ξ₁, ξ₂) может служить некоторой мерой зависимости между двумя случайными величинами. Чаще в качестве такой меры принимают безразмерный коэффициент корреляции

Две случайные величины, для которых коэффициент корреляции равен нулю, называются некоррелированными. Случайные величины, для которых 1-й начальный момент их произведения

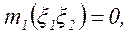
называют ортогональными. Если средние значения случайных величин равно нулю, то понятия ортогональности и некоррелированности случайных величин совпадают.

Моменты распределения того или иного порядка, являясь важными числовыми характеристиками случайной величины, не являются, однако, их однозначной полной статистической характеристикой: случайные величины, имеющие одинаковые 1-й и 2-й моменты, могут иметь разные законы распределения.

Дата добавления: 2014-12-07