Моя поездка в горы состоится лишь при условии, что я достану путёвку в лагерь и не будет аврала на работе

Здесь предполагается, что поездка в горы (G) есть логическая функция двух аргументов – аврала (A) и путёвки (Р). По смыслу высказывания очевидно, что:

· если А=0 и Р=0, то G=0;

· если А=0 и Р=1, то G=1;

· если А=1 и Р=0, то G=0;

· если А=1 и Р=1, то G=0.

Весь этот набор фактов принято записывать в виде таблицы:

A	P	G

Такая таблица полностью и однозначно описывает логическую функцию. Таблица, где перечислены обязательно все возможные (!) значения логической функции, называется таблицей истинности.

Количество строк в таблице истинности напрямую связано с числом аргументов функции. Если аргументов два, в таблице будет четыре строки, при трёх аргументах – восемь строк, при четырёх – шестнадцать, при N аргументах - 2^N строк. Чтобы не ошибиться при перечислении всех возможных наборов значений аргументов, эти наборы всегда следует располагать в порядке возрастания натурального ряда чисел, записанных в двоичной системе счисления, начиная с нуля. Так, при двух аргументах (А и Р в предыдущем примере) этими наборами будут 00, 01, 10, 11. В случае трёх аргументов будем иметь наборы 000, 001, 010, 011, 100, 101, 110, 111. По аналогии с обычной (классической) математикой можно сказать, что эти наборы образуют область определения функции.

Отметим, что, в отличие от классической математики, где область определения функции может содержать (чаще всего так и бывает) бесконечное множество чисел, область определения логической функции всегда конечна. Именно поэтому и возможно полностью описать логическую функцию с помощью таблицы. Число самих логических функций от N аргументов также конечно. Оно равно в точности . Так, при трёх аргументах может существовать не более 256 различных логических функций.

Множество, состоящее из трёх логических функций с названиями «НЕ». «И», «ИЛИ», называется стандартным, каноническим или булевским базисом в честь уже известного нам Джорджа Буля, подробно исследовавшего эти функции.

Функция НЕ, или инверсия, отрицание – самая простая их всех. По определению, она равна 1, если её единственный аргумент равен 0, и равна 0, если аргумент равен 1. Таблица истинности этой функции, очевидно, состоит из двух строк, и мы не будем её рассматривать. Электронный логический элемент, реализующий эту функцию, называется инвертор. Он имеет один вход и один выход.

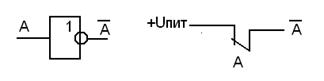
На рисунке ниже приведено условное графическое изображение инвертора (обратите внимание на кружок на выходе), а также его наглядная реализация в виде размыкающего контакта реле. Этот контакт замкнут (1), когда в обмотке реле нет тока (0), и наоборот, разомкнут (0), когда ток есть (1). На этом же рисунке приведено наиболее распространённое условное обозначение самой функции отрицания А, а именно «А с чертой сверху». Существуют и другие обозначения, например, Not(A), в школьном курсе информатики эта функция обозначена A.

Функция И (по-другому называемая конъюнкция), по определению, равна 1 тогда и только тогда, когда все её аргументы (их может быть два или более) равны 1. Функция называется также логическим умножением, обозначается как A&B (& - знак амперсанд), либо A·B, либо просто AB. Встречается также крайне неудобное обозначение (принятое, к сожалению, в школьном курсе информатики) AΛB. Соответствующий логический элемент называется конъюнктор.

На рисунке ниже приведено два условных графических обозначения конъюнктора – для случая двух и четырёх входов (теоретически их может быть любое количество, большее или равное 2), а также наглядная реализация в виде последовательно включённых замыкающих контактов реле. Электрический сигнал на выходе такой цепочки будет, очевидно, если замкнут и первый, и второй контакт.

Функция ИЛИ (также называемая дизъюнкция), по определению, равна 1 тогда и только тогда, если хотя бы один её аргумент (их может быть, как и в предыдущем случае, два или более) равны 1. Эта функция называется также логическим сложением, обозначается AVB (здесь V – это знак ИЛИ), а также иногда A+B, хотя такое обозначение нельзя признать удачным. Соответствующий логический элемент называется дизъюнктор. На рисунке ниже приведено два условных графических обозначения дизъюнктора – опять же для случая двух и четырёх входов, а также наглядная реализация в виде параллельно включённых замыкающих контактов реле. Электрический сигнал на выходе такой цепочки будет, очевидно, если замкнут или первый, или второй контакт, или оба сразу.

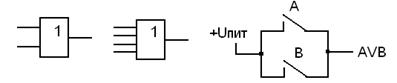
Таблица истинности для случая двух аргументов A и B приведена ниже. Кроме уже знакомых нам И, ИЛИ, в таблицу включены также значения функции «сложение по модулю два» (кратко обозначенную M2), а также широко используемых на практике комбинированных функций И-НЕ (обозначено NAND – от Not And), ИЛИ-НЕ (обозначено NOR – от Not Or).

A	B	A&B	AVB	M2	A NAND B	A NOR B

Рассмотренный булевский базис (набор функций) И, ИЛИ, НЕ обладает свойством полноты – это означает, что с помощью только этих функций можно выразить любую функцию алгебры логики, сколь бы сложной она ни была (отметим, что существуют и другие базисы с этим же свойством). Соответственно, при помощи одних только конъюнкторов, дизъюнкторов и инверторов можно (в принципе) построить логическую схему любого цифрового устройства, работа которого описывается в терминах алгебры логики!

Отметим, что приведённые выше обозначения логических элементов относятся к так называемой европейской системе. В отечественном школьном курсе информатики (Угринович Н.Д. и др.) используется другая символика, а именно:

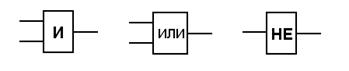
Студенты, не занимавшиеся ранее цифровой электроникой, скорее всего, знакомы именно с этими обозначениями, оставшимися в памяти после школы. В инженерной литературе они практически не применяются. Существует также и американская система обозначений элементов, рассматривать которую здесь не будем.

Тема 2. Построение и моделирование логических схем

Представление логической функции в виде таблицы истинности – не единственно возможное. Располагая такой таблицей, можно получить представление функции в виде формулы, а затем, если это необходимо, построить по этой формуле логическую схему устройства, реализующего данную функцию.

Пусть дана таблица истинности для какой-то функции трёх переменных (здесь для экономии места таблица разбита на две части, размещённые рядом):

A	B	C	F	A	B	C	F

Мы видим, что столбец F заполнен нулями и единицами, в этом наборе оказалось три единицы, все остальные – нули. Откуда взялись эти данные? Они определяются постановкой задачи на разработку конкретного цифрового устройства. Сейчас наша цель – перейти от таблицы к формуле.

Делается это очень просто. Для каждой строки таблицы, содержащей 1 в столбце F, следует выписать так называемую элементарную конъюнкцию трёх входных переменных. Переменные A, B, C соединяем знаком конъюнкции (то есть попросту пишем переменные рядом, как при операции умножения) и затем ставим знак инверсии (черту над буквой) там, где во входном наборе переменных стоит ноль, и оставляем без инверсии там, где стоит единица:

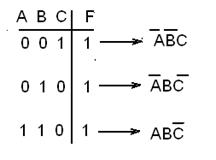
Теперь полученные элементарные конъюнкции соединяем, как слагаемые в обычной алгебре, знаками дизъюнкции:

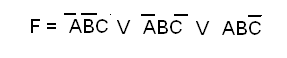
Выражение, которое у нас получилось, носит название совершенная дизъюнктивная нормальная форма (сокращённо СДНФ). Это и есть искомое представление логической функции в виде формулы. СДНФ всегда содержит ровно столько слагаемых, сколько единиц в таблице истинности; каждое слагаемое содержит обязательно все переменные, причём каждая из них входит в формулу либо непосредственно, либо в виде инверсии.

Существуют также представления логической функции в виде ДНФ (дизъюнктивных нормальных форм, без слова «совершенный»), когда каждое слагаемое содержит не обязательно все переменные.

Следующий шаг – это переход от СДНФ к логической схеме.

Стандартный вид логической схемы, построенной по СДНФ (и вообще любой ДНФ) – это так называемая трёхъярусная структура. В первом ярусе схемы располагаются инверторы (в нашем случае 555LN1); их количество не превосходит количества переменных-аргументов функции, Второй ярус образуют конъюнкторы (в нашем случае 555LI3); их число равно количеству слагаемых (элементарных конъюнкций). Наконец, третий ярус – это дизъюнктор, вырабатывающий выходной сигнал функции:

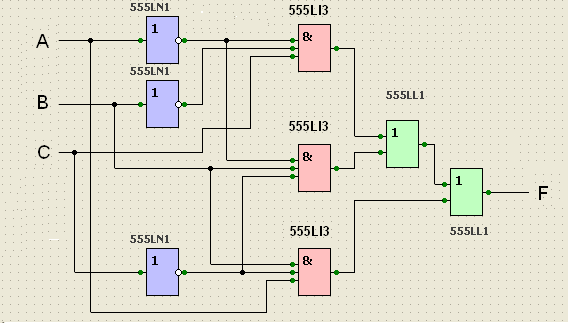
При построении этой схемы было учтено, что в учебной библиотеке логических элементов TTL.SLB системы PCAD нет, к сожалению, дизъюнктора с тремя входами, поэтому в третьем ярусе применено каскадное включение двух дизъюнкторов с двумя входами каждый (а именно 555LL1).

Схема построена. Уже в таком виде её можно моделировать в системе PCAD, хотя в дальнейшем мы будем подвергать её существенной доработке. Работа с этой системой описана в отдельном пособии, кроме того, самые необходимые сведения будут приведены ниже. Мы будем предполагать, что исходный файл со схемой, построенный в программе-редакторе схем PCCAPS, имеет имя F31.SCH, из которого после обработки программами PCNODES и PRESIM получился файл F31.NET.

Рекомендуем использовать следующее содержимое CMD-файла:

Дата добавления: 2014-12-07