Общая постановка задачи

СИМПЛЕКСНЫЙ МЕТОД

Если задача линейного программирования имеет оптимальное решение, то оно соответствует хотя бы одной угловой точке ОДР и совпадает, по крайней мере, с одним допустимым базисным решением. Поэтому для решения ЗЛП можно перебрать все допустимые базисные решения и выбрать среди них то, на котором целевая функция принимает оптимальное значение. Геометрически это означает перебор всех угловых точек ОДР. Однако практическое осуществление такого подхода связано с огромными трудностями, так как число допустимых базисных решений хотя и конечно, но может быть очень велико.

Симплексный метод позволяет существенно сократить количество перебираемых базисных решений, так как перебор производится целенаправленно. При этом каждое последующее решение, по крайней мере, «не хуже» предыдущего. Поясним это на графическом примере.

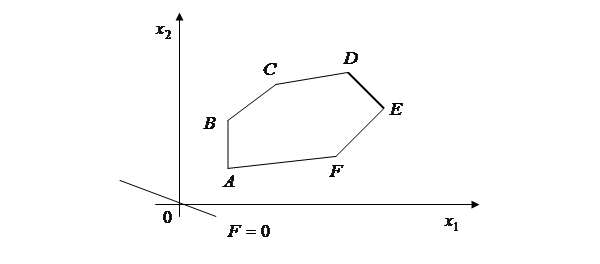
Рис. 9

Предположим, что точка 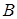соответствует исходному допустимому базисному решению. Тогда при беспорядочном переборе пришлось бы проверить шесть угловых точек. Однако по рис. 9 видно, что выгодно из точки перейти к точке и затем к оптимальной точке . То есть вместо шести точек перебрали только три.

Таким образом, идея симплексного метода (или метода последовательного улучшения решения) заключается в том, что начиная с некоторого исходного опорного решения осуществляется целенаправленное перемещение по опорным решениям к оптимальному. Значения целевой функции при таком перемещении не убывают (возрастают) для задач на максимум, и не возрастают (убывают) для задач на минимум.

Следовательно, для реализации симплексного метода необходимо освоить три элемента:

1) Способ определения первоначального допустимого решения.

2) Правило перехода к лучшему (не худшему) решению.

3) Критерий проверки оптимальности найденного решения.

Рассмотрим применение симплексного метода на примерах.

Дата добавления: 2014-12-07