Суммарные допуски и отклонения формы и расположения поверхностей

Суммарным отклонением формы и расположенияЕС называется отклонение, являющееся результатом совместного проявления отклонения формы и отклонения расположения рассматриваемой поверхности или рассматриваемого профиля относительно баз.

Поле суммарного допуска формы и расположении ТС – это область в пространстве или на заданной поверхности, внутри которой должны находиться все точки реальной поверхности или реального профиля в пределах нормируемого участка. Это поле имеет заданное номинальное положение относительно баз.

Различают следующие виды суммарных допусков:

- радиальное биение поверхности вращения относительно базовой оси является результатом совместного проявления отклонения от круглости профиля рассматриваемого сечения и отклонения его от центра относительно базовой оси; оно равно разности наибольшего и наименьшего расстояний от точек реального профиля поверхности вращения до базовой оси в сечении, перпендикулярной этой оси (∆);

- торцовое биение – разность ∆ наибольшего и наименьшего расстояний от точек реального профиля торцовой поверхности до плоскости, перпендикулярной базовой оси; определяется на заданном диаметре d или любом (в том числе и наибольшем) диаметре торцевой поверхности;

- биение в заданном направлении – разность ∆ наибольшего и наименьшегорасстояний от точек реального профиля поверхности вращения в сечении рассматриваемой поверхности конусом, ось которого совпадает с базовой осью, а образующая имеет заданное направление, до вершины этого конуса;

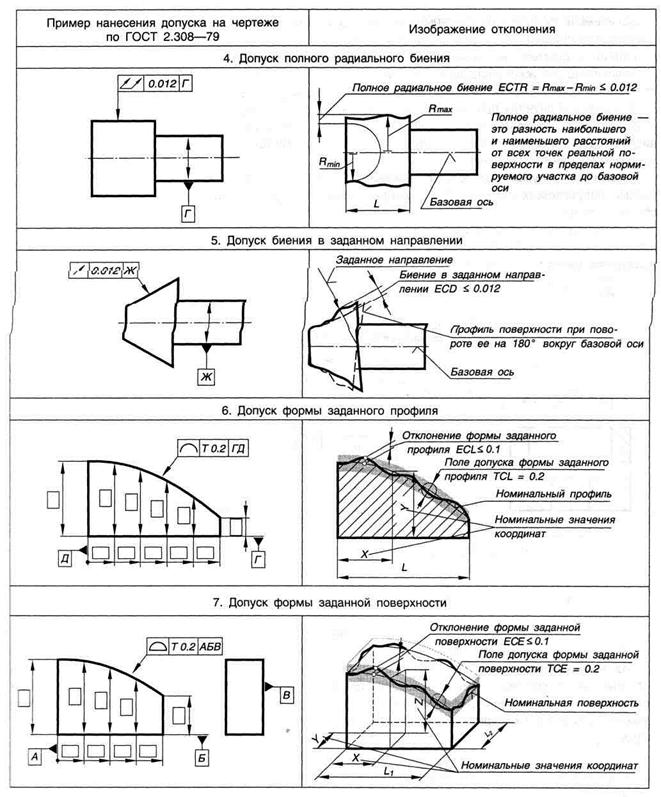
- полное радиальное биение – разность ∆ наибольшего R_max и наименьшегоR_min расстояний от всех точек реальной поверхности в пределах нормируемого участка L до базовой оси;

- полное торцовое биение – разность ∆ наибольшего и наименьшегорасстояния от точек всей торцовой поверхности до плоскости, перпендикулярной базовой оси;

- отклонение формы заданного профиля – наибольшего отклонения ∆ точек реального профиля, определяемое по нормали к нормируемому профилю в пределах нормируемого участка L;

- отклонение формы заданной поверхности – наибольшее отклонение ∆ точек реальной поверхности от номинальной поверхности, определяемое по нормали к номинальной поверхности в пределах нормируемого участка L₁, L₂

Виды допусков, их обозначение и изображение на чертежах приведены в таблицах 5 и 6.

Таблица 5 – Виды суммарных допусков и их условное изображение

Таблица 6 – Примеры изображения суммарных допусков на чертежах

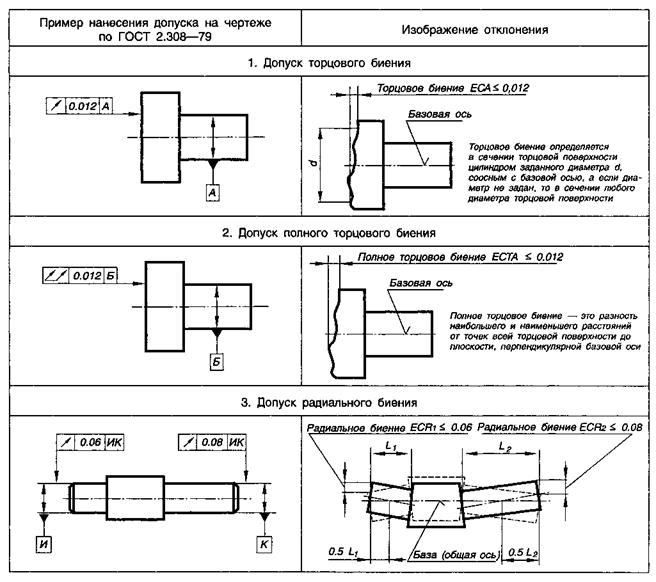
Продолжение таблицы 6

Форма и размеры знаков, рамки и изображения баз приведены на рисунке 11

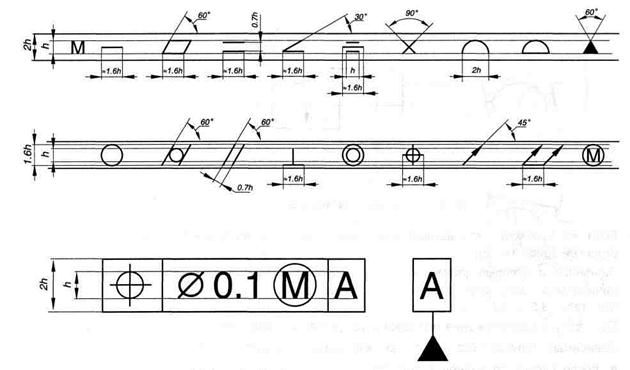
Рисунок 11 – Форма и размеры знаков, рамки изображение баз

Дата добавления: 2014-12-07