Аналитические методы вычисления процессов

Аналитические методы вычисления выходного сигнала замкнутой системы базируются на известных методиках решения дифференциальных уравнений. Решение (4.1) классическими методами во временной области приводит к соотношению (4.7). Зная 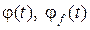, внешние воздействия v (t), f (t) и интегрируя (4.7), можно вычислить реакцию системы y (t). такой подход редко используется в практике теории управления, а выражение (4.7) в большей степени применяется в теоретических выкладках.

На практике решение уравнения (4.1) чаще всего осуществляют с помощью операционного исчисления на базе преобразования Лапласа, т.е. за основу принимают выражение (4.2).

Рассмотрим методику вычисления реакции системы на внешнее воздействие v (t) при нулевых начальных условиях координаты у (t) и ее производных. В этом случае связь изображений входа и выхода будет иметь вид

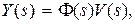(4.8)

где в общем случае 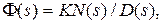N (s) и D (s) – полиномы степени m и n соответственно.

Вычисление составляющей 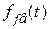, обусловленной возмущением f (t), будет аналогичным с использованием передаточной функции .

В (4.8) изображение v (s)длябольшинства типовых воздействий представляет собой дробно-рациональную функцию, т.е.также является отношением некоторых полиномов относительно s. Таким образом, изображение Y (s) в этом случае будет иметь следующий вид: 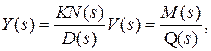где степень полинома M (s) меньше степени полинома Q(s), которую обозначим через r и в общем случае .

Вычисление оригинала y (t) по его изображению осуществляется по формулам разложения Xевисайда. Если полюса изображения Y (s), являющиеся корнями уравнения 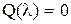, которые обозначим 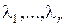, являются различными, то оригинал определяется выражением

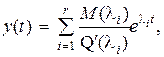(4.9)

где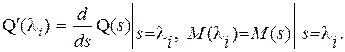

B случае кратных полюсов для вычисления оригинала используется выражение на основе вычетов [6].

Если входной сигнал v (t) = 1[ t ], то , а изображение реакции системы в соответствии с (4.8) примет такой вид: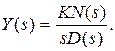

Реакция системы в этом случае является переходной функцией замкнутой системы h_з (t), которая как частный случай (4.9) будет вычисляться по выражению

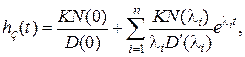(4.10)

где 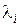– различные корни характеристического уравнения замкнутой системы.

Следует отметить, что случай кратных корней при исследовании систем управления встречается сравнительно редко.

В (4.10) 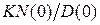характеризует так называемую установившуюся составляющую, а 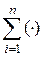– переходную составляющую. И вобщем случае в (4.9) для произвольного процесса y (t) можно всегда выделить две составляющие: установившуюся 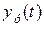и переходную . Частным случаем установившейся составляющей является случай, соответствующий 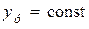, которую будем называть статической составляющей. Для асимптотически устойчивых систем (это понятие будем рассматривать в разд. 5) всегда 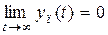и при больших значениях t реакция системы .

Отметим, что так как в (4.10) 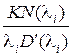– это постоянные величины, то структура переходной составляющей 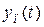идентична структуре свободной составляющей 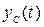(4.4).

Реакция системы y (t) на входнойсигнал v (t) при нулевых начальных условиях определяется выражением .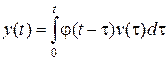

Для вычисления установившейся составляющей можно воспользоваться выражением [1]:

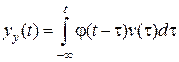
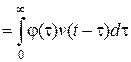. (4.11)

При гармоническом входном сигнале для вычисления установившейся составляющей можно использовать частотные характеристики системы. Пусть на входе системы v (t) 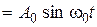, тогда установившееся значение выходного сигнала будет также гармоническим сигналом и может быть вычислено по выражению

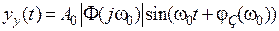, (4.12)

где 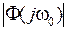– значение АЧХ, a 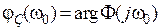– значение ФЧХ замкнутой системы при .

Пример 4.2. Рассмотрим систему управления, структура которой представлена на рис. 3. 1. Как и в предыдущем примере, 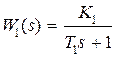, 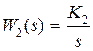. Пусть Т ₁ = 0,01 c; K ₁ = 10; K ₂ = 0,475. Входной сигнал v (t) = 1[ t ].

С учетом изображения входного сигнала найдем .

Используя (4.10) с учетом того, что характеристическое уравнение 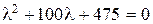имеет два различных корня 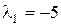, , получим .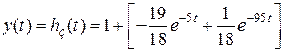

Из полученного выражения следует, что переходная составляющая с течением времени затухает, а установившаяся – постоянна и равна единице.

Вычислим установившуюся составляющую выходного сигнала при гармоническом входном сигнале 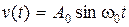, 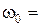10 рад/c, Т ₁ = 0,25 c, K ₁ K ₂ = 25. Передаточная функция имеет вид 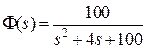, откуда, заменяя s на 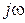, получим , .

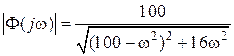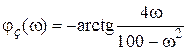при 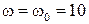значения и рад. Tаким образом, установившееся значение выходного сигнала будет равно .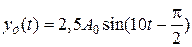

Применение аналитических методов на практике ограничено из-за необходимости вычисления корней характеристического уравнения, построения по найденному аналитическому выражению переходной функции, нахождения показателей качества системы (tp, 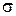и др.). Чтобы обойти эти трудности, были разработаны приближенные графические методы построения переходной функции, вытекающие из связи h_з (t) с вещественной частотной характеристикой замкнутой системы :

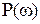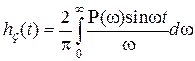. (4.13)

Выражение (4.13) положено в основу приближенных графических методов построения 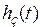. Суть этих методов заключается ваппроксимации характеристик 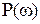и вычислении соответствующих составляющих переходного процесса. Например, А. А. Вороновым был предложен метод аппроксимации 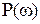с помощью треугольных, а В. В. Солодовниковым – с помощью трапецеидальных характеристик.

Однако в связи с развитием вычислительной техники в настоящее время графо-аналитический метод вычисления переходной функции утратил свое прежнее значение. Переходной процесс любой САУ легко строится при проведении компьютерного эксперимента, например, в системе Matlab с помощью стандартных функций или с использованием средства Simulink после создания соответствующей математической модели исследуемой системы.

Дата добавления: 2014-12-07