Построение областей устойчивости

Устойчивость замкнутой системы зависит от корней характеристического уравнения

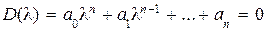. (5.14)

Пусть при определенных значениях коэффициентов все корни уравнения (5.14) будут левыми. Изменяя коэффициенты 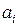, будем получать то или иное расположение корней на комплексной плоскости. Совокупность всех значений коэффициентов 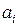, для которых все корни уравнения (5.14) являются левыми, образует область устойчивости системы в пространстве коэффициентов характеристического уравнения.

Так как коэффициенты уравнения (5.14) являются функциями параметров системы (коэффициентов усиления, постоянных времени и т.п.), то аналогично можно говорить об областях устойчивости в пространстве параметров
системы.

Обычно такие области строятся при изменении одного или двух параметров системы, так как при большем числе параметров геометрическая интерпретация областей теряет наглядность.

Вполне очевидно, что для построения областей устойчивости достаточно найти только лишь ее границу и показать, что хотя бы для одной из внутренних точек области все корни будут являться левыми.

Границы устойчивости могут быть найдены с помощью любого критерия (Гурвица, Михайлова). Так, в примере 5.3 с помощью критерия Гурвица найдены границы области устойчивости в пространстве трех параметров от 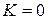до , , .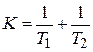

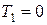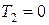Однако для выделения областей устойчивости разработан специальный метод D-разбиения, предложенный Ю. Неймарком. рассмотрим этот метод.

Корень уравнения (5.14) попадает на мнимую ось (границу устойчивости в плоскости корней), если 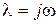является решением уравнения (5.14), т.е. выполняется равенство

. (5.15)

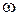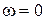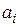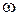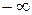Если задано ( соответствует нулевому корню), то (5.15) можно рассматривать как уравнение относительно искомых коэффициентов , при которых один корень находится на границе устойчивости. Изменяя от до 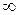в пространстве коэффициентов 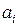, получим некоторую поверхность, соответствующую границе устойчивости (попаданию корня уравнения (5.15) на мнимую ось). Эта поверхность разобьет все пространство коэффициентов на области с определенным расположением левых и правых корней, которые обозначим 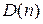, ,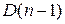…, 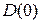. Область 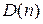соответствует n корням в правой полуплоскости, 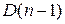– – 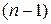корню в правой полуплоскости и т.д. Область D (0) соответствует n корням в левой полуплоскости, т.е. области устойчивости. При пересечении границы, определяемой уравнением (5.15), происходит переход корня из левой полуплоскости в правую или наоборот.

Рассмотрим частный случай: D -разбиение по одному комплексному параметру. Пусть исследуемый параметр линейно входит в уравнение (5.14), которое в этом случае приводится к виду 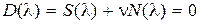, а граница области D -разбиения определяется уравнением 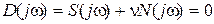, откуда, полагая 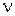комплексной величиной и обозначая ее 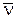, получим .

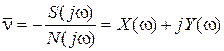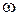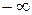Границу D -разбиения в комплексной плоскости строим, изменяя от до 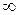, которая будет представлять собой некоторую кривую. При изменении 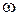от 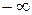до 0 кривая будет зеркальным отображением относительно действительной оси кривой при .

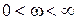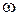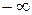При движении вдоль границы D -разбиения ее штрихуют слева, двигаясь при изменении от до 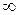, что соответствует в плоскости корней движению вдоль мнимой оси снизу вверх так, что левая полуплоскость корней остается слева.

На рис. 5.9 изображена кривая D -разбиения в комплексной плоскости.

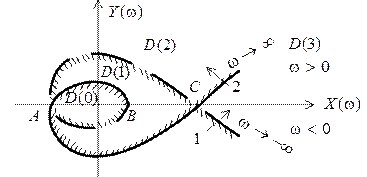
Рис. 5.9

Пересечение границы D -разбиения из заштрихованной стороны в незаштрихованную сторону (стрелка 1 на рис. 5.9) соответствует переходу одного корня из левой полуплоскости в правую. Стрелка 2 соответствует переходу правого корня в левую полуплоскость плоскости корней.

Обычно претендентом на область устойчивости является область, внутрь которой направлена штриховка, соответствующая наибольшему количеству левых корней. На рис. 5.9 это область, включающая отрезок АВ. Для проверки, является ли эта область областью устойчивости 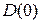, берут любое значение исследуемого параметра 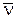из этой области, подставляют его в исходное характеристическое уравнение и с помощью любого критерия проверяют устойчивость. Так как на практике исследуемый параметр является действительным, то из полученной области устойчивости выделяют только действительные значения 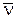. Это будет отрезок АВ. На рис. 5.9 также показаны области .

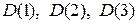Пример 5.5. Рассмотрим систему автоматического управления из
примера 5.3. Построим кривую D -разбиения по одному параметру – коэффициенту K. Характеристическое уравнение замкнутой системы имеет вид

.

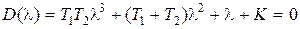Заменяя 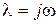, получим 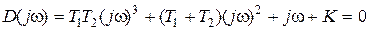, откуда, считая K комплексным, получим .

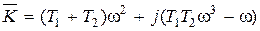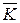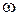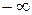В комплексной плоскости параметра при изменении от до 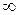будем иметь кривую, изображенную на рис. 5.10.

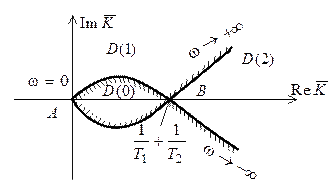
Рис. 5.10

В точке В величина 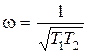, a 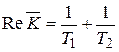. Областью устойчивости будет область 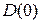, что определяется с помощью критерия Гурвица. Так как
K – действительная величина, то получаем отрезок устойчивости АВ, т.е. область устойчивости будет определяться неравенством 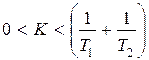, что совпадает с результатом примера 5.3.

Дата добавления: 2014-12-07