Установившиеся ошибки при произвольном входном сигнале

Обозначим весовую функцию замкнутой системы по ошибке через 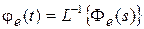. Тогда соотношению во временной области будет соответствовать свертка .

Так как нас интересует установившаяся ошибка после затухания переходной составляющей, то отнесем нижний предел интегрирования, соответствующий моменту подачи входного сигнала, в 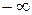. В этом случае получим выражение, справедливое для установившегося значения сигнала ошибки: .

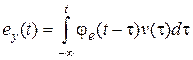Заменив переменную интегрирования , получим

. (6.7)

Полагая функцию 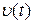аналитической, разложим ее в ряд Тейлора при 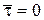: 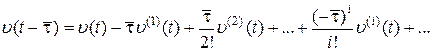и подставим полученный ряд в (6.7). В результате получим

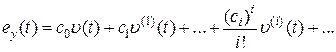, (6.8)

где коэффициенты определяются выражением .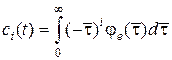

Так как передаточная функция замкнутой системы по ошибке есть прямое преобразование Лапласа от весовой функции , то очевидно соотношение

. (6.9)

Коэффициенты носят название коэффициентов ошибок и характеризуют, с каким весом функция 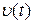и ее производные входят в общее выражение для установившейся ошибки (6.8). Если входной сигнал изменяется достаточно медленно, то в выражении (6.8) можно ограничиться конечным числом членов ряда.

Если , то . В статической системе и , для системы с астатизмом первого порядка имеем 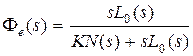и , а

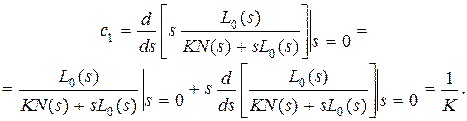
Аналогично можно показать, что для астатической системы с астатизмом 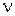-го порядка , .

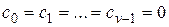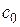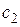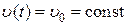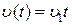Коэффициент называют коэффициентом статической ошибки, – коэффициентом скоростной ошибки, – коэффициентом ошибки по ускорению. Из (6.8) следует, что если , то , если , то .

В общем случае формула (6.9) редко используется для вычисления 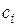. На практике применяется другой способ. Разложим передаточную функцию 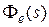в ряд Маклорена при s = 0:

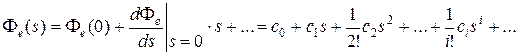. (6.10)

С другой стороны, так как есть отношение полиномов, то деля полином числителя на полином знаменателя, получим ряд

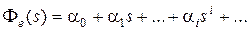. (6.11)

Приравнивая коэффициенты при одинаковых степенях s в (6.10), (6.11), получим

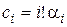. (6.12)

Величина коэффициентов ошибок в конечном итоге определяет величину ошибки в системе. Из изложенного выше вновь следует, что величины 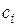будут тем меньше, чем выше порядок астатизма системы и чем больше величина коэффициента усиления K разомкнутой системы.

Пример 6.2. Пусть передаточная функция разомкнутой системы имеет вид 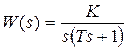. Найдем первые три коэффициента ошибок. Передаточная функция замкнутой системы по ошибке будет равна 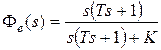. Деля полином числителя на полином знаменателя, получим .

В соответствии с (6.12) найдем , , .

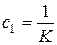Определим установившуюся ошибку в системе при воздействии . Подставляя найденные значения 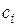и заданные значения функции и ее производных в (6.8), получим .

Дата добавления: 2014-12-07