Статистический анализ в методе сравнения продаж

Определение МВР

Сопоставимые объекты	Цена продажи, долл.	Рентный годовой доход, долл.	МВР
	60 000		15,19
	61 800		15,07
	63 700		16,33
			16,10
			15,88
			15,26
	61 000		16,05

Принципиально важно отметить, что расчет МВР и рыночного рентного дохода для оцениваемого объекта проводится не обязательно по одним и тем же сравнимым объектам, хотя отдельные объекты могут быть использованы для обоснования рыночного рентного дохода для оцениваемого объекта (в табл. 9.7 из табл. 9.6 вошел сравнимый объект с арендной платой в 4200 долл.).

Расчетный показатель рыночного рентного дохода для оцениваемого объекта составляет 4100 долл. в год. Тогда рыночная стоимость оцениваемого односемейного жилого дома, сдаваемого в аренду отдыхающим, равна 4100 х 15,88 = 65 108 долл.

Статистические характеристики. В практической оценочной деятельности находит широкое применение аппарат математической статистики. При анализе статистических данных о сделках купли-продажи недвижимости важное место занимают статистические характеристики (средние величины и показатели вариации), которые позволяют судить о характерных особенностях наблюдаемого статистического ряда. В качестве средних величин используют среднюю арифметическую, медиану и моду.

Таблица 9.7

Корректировка арендной платы по сравнимым объектам и определение рыночного рентного дохода для оцениваемого объекта (в долл.)

Элемент сравнения	Оцениваемый объект	Объект I	Объект II	Объект III	Объект IV
Арендная плата
Ванная комната	Есть	Нет	Корректировка 400	Нет	Корректировка 400	Есть	Корректировка 0	Нет	Корректировка 400
Гараж	Есть	Нет	Корректировка	Есть	Корректировка	Есть	Корректировка	Есть	Корректировка
Центральное отопление	Нет	Нет	Корректировка0	Нет	Корректировка	Есть	Корректировка -400	Есть	Корректировка
Оплата коммунальных услуг	Арендатором	Арендатором	Корректировка	Арендатором	Корректировка	Арендатором	Корректировка	Владельцем	Корректировка -500
Абсолютная корректировка				-400	-100
Показатель рыночного рентного дохода в год

Средняя арифметическая,по данным наблюдений, равна

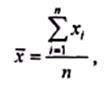(9.1)

где х — средняя арифметическая;

x₁, х₂,..., x_n — данные наблюдений;

n — число наблюдений.

Медианой называют значение признака, приходящегося на середину ранжированного ряда наблюдений.

Модой называют такое значение признака, которое наблюдалось наибольшее число раз.

Рассмотрим статистическую выборку из девяти квартир, имеющих кухни следующих размеров (м²): 5; 8,5; 6; 9,5; 10; 8; 6,5; 6,5; 9. Используя формулу (9.1), получим среднее значение размера кухни этой выборки, равное 7,7 м². Для определения значения медианы ранжируем рассматриваемый статистический ряд: 5; 6; 6,5; 6,5; 8; 8,5; 9; 9,5; 10. Согласно определению медианы ее значение будет соответствовать кухне размером 8 м². Проанализировав представленную статистическую выборку, нетрудно определить значение моды, которое будет соответствовать кухне размером 6,5 м².

Итак, мы получили три средние величины для рассматриваемой статистической выборки: 7,7; 8 и 6,5 м². Эти представленные средние величины различаются в диапазоне 8—6,5 м², и в этой связи возникает необходимость выбора одного среднего значения. В практической деятельности оценщика для проведения статистического анализа конкретного статистического ряда применение указанных выше средних величин проводится в следующем порядке. В случае, если статистическая выборка по размерам (по числу наблюдений) достаточно велика, для экспресс-анализа в качестве средней величины удобнее выбрать моду (не требуется никаких вычислительных процедур). Если таковой в выборке нет, то после ранжирования статистического ряда можно определить значение медианы. Наконец, если оценщик ставит перед собой задачу уточненного расчета среднего значения рассматриваемой статистической выборки, можно воспользоваться алгоритмом расчета по формуле (9.1).

Показатели вариации. Средние величины характеризуют статистический ряд числом, но не отражают изменчивость наблюдавшихся значений признака, т. е. вариацию. В практической деятельности оценщика в качестве описательных характеристик показателей вариации в основном используются значения стандартного S_x и среднеквадратичного отклонения а_x:

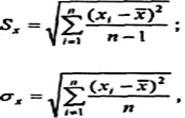(9.2)

(9.3)

где х — средняя арифметическая;

х₁, х₂,..., х_n — данные наблюдений;

n — число наблюдений.

Для проведения соответствующих расчетов, как правило, оценщик применяет специальный калькулятор, имеющий статистическую таблицу. В частности, калькулятор "Texas Instruments B II PLUS" посредством введения статистических данных (до 50 значений) позволяет вычислить среднее значение х, стандартное отклонение S_x и среднеквадратичное а_x.

Применение аппарата математической статистики в методе сравнения продаж предполагает проведение также корреляционно-регрессионного анализа. На основе статистических данных о рыночных продажах недвижимости и выявленных факторов, наиболее существенно влияющих на стоимость недвижимости, определяется корреляционная связь (теснота) между ценой продажи и соответствующим фактором. Далее, с помощью анализа соответствующих статистических характеристик определяется вид уравнения регрессии (модель), которое позволит исчислить оценку рассматриваемого объекта недвижимости в зависимости от количественных (и качественных) значений введенных в уравнение факторов (независимых переменных).

Проиллюстрируем применение корреляционно-регрессионного анализа для определения оценки недвижимости на следующем примере.

ПРИМЕР

Для оцениваемого офиса общей площадью 84,5 м² оценщик обнаружил 10 сопоставимых продаж, данные которых приведены в табл. 9.8.

Таблица 9.8

Дата добавления: 2014-12-07