В длинной линии без потерь

Анализ гармонических колебаний

Анализ переходных колебаний в электрической цепи

классическим методом

Найдите закон изменения напряжения и тока на реактивном элементе u_C(t), i_C(t) или u_L(t), i_L(t) после коммутации при условии, что до коммутации в цепи был установившийся режим.

Для этого:

1. Выберите для своего варианта схему цепи и рассчитайте её параметры через Mи Nиз табл. 1.4, если последняя цифра номера зачётной книжки нечётная, или из табл. 1.5, если – чётная (цифру 0 считать чётной).

2. Составьте для схемы, получившейся после коммутации, систему уравнений по законам Кирхгофа для мгновенных значений токов и напряжений и получите одно дифференциальное уравнение относительно u_C(t) или i_L(t).

3. Найдите путём решения полученного дифференциального уравнения искомую реакцию цепи u_C(t) или i_L(t), по которой определите i_C(t) или u_L(t) соответственно.

4. Постройте графики функций u_C(t), i_C(t) или i_L(t), u_L(t).

Таблица 1.4

Таблица 1.5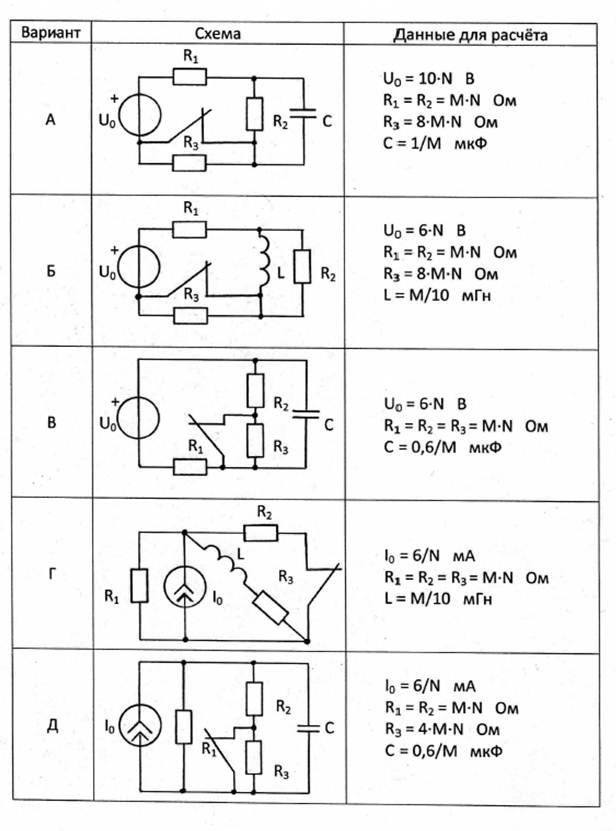

Задача 6

Воздушная длинная линия без потерь состоит из двух участков с одинаковым волновым сопротивлением ρ, напряжение на входе линии u₁(t) = U₁√2cos(2πft).

Первичные параметры каждого участка выбраны так, что фазовая скорость V_ф, а, следовательно, и длина волны λ на всех участках одинакова. В соответствии со своим вариантом выберите схему линии в табл. 1.6 и рассчитайте параметры линии и нагрузок через M и N.

Для этого:

1. Рассчитайте входное сопротивление Z_вх2 и определите режим работы линии длиной l₂.

2. Рассчитайте сопротивление нагрузки Z’₂ линии длиной l₁ как параллельное соединение Z₁ и Z_вх2 и вычислите значение коэффициента отражения линии длиной l₁.

3. Рассчитайте входное сопротивление Z_вх1 и определите режим работы линии длиной l₁.

4. Рассчитайте действующие значения токов и напряжений в линии: I₁, U’₂, I’₂, U₂, I₂.

5. Рассчитайте распределение действующего значения напряжения вдоль каждого участка линии, выбрав не менее пяти расчётных точек в промежутке от y = 0 до y = λ\4. Постройте отдельно для каждого участка линии графики распределения действующего значения напряжения U(y) в пределах изменения y: 0 ≤ y≤ l₁; 0 ≤ y≤ l₂.

6. Рассчитайте значение коэффициента бегущей волны К_БВ в линии длиной l₁.

7. Определите ближайшее резонансное сечение y_рез от конца линии длиной l₁ и величину сопротивления R_рез в этом сечении.

Таблица 1.6

8. Для вариантов А, Б, В, Г определите значение сопротивления R, которое надо подключить вместо Z₁, чтобы в линии длиной l₁ установился режим бегущей волны. Нарисуйте качественный график распределения действующего значения напряжения вдоль линии длиной l₁ при выбранном R.

9. Для варианта Д рассчитайте входное сопротивление Z_вх2 и определите режим работы линии длиной l₂ при условии, что Z₂ = 0. Нарисуйте качественный график распределения действующего значения напряжения вдоль линии длиной l₂ при Z₂ = 0. Сделайте вывод, изменится ли режим работы участка линии длиной l₁ при Z₂ = 0 и почему.

ЛИТЕРАТУРА

1. Белецкий А.Ф. Теория линейных электрических цепей: Учебник. 2-е изд. – СПб.: Издательство «Лань», 2009. – 544 с.

2. Бакалов В.П., Дмитриков В.Ф., Крук Б.И. Основы теории цепей: Учебник для вузов; Под редакцией В.П. Бакалова. 3-е изд. – М.: Горячая линия – Телеком, 2009. – 596 с.

Дата добавления: 2014-12-07