Термодинамика потока в каналах переменного сечения

Замена переменных приводит уравнение к виду

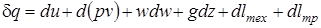. (2.36)

Напишем уравнение первого закона термодинамики в виде

. (2.37)

Далее приравнивая правые части уравнений (2.36 и 2.37), с учетом, что , получаем

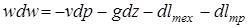. (2.38)

Последнее дифференциальное уравнение представляет математическую запись первого закона термодинамики для потока.

В конкретном характерном случае (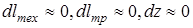) эта зависимость принимает вид:

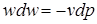. (2.39)

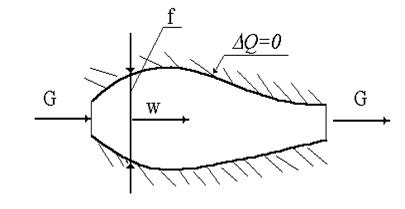Рис. 2.10

Каналы переменного сечения, в которых происходит расширение рабочего тела и увеличение скорости потока, называются соплами (конфузорами). Они применяются для получения высоких скоростей и струй ударного действия.

Каналы переменного сечения, в которых происходит сжатие рабочего тела, сопровождающееся с ростом давления, называются диффузорами. Их используют в конструкциях насосов, вентиляторов и др.

Основой вывода общих закономерностей движения рабочего тела в каналах переменного сечения является уравнение неразрывности потока, которое при стационарном режиме движения (при G= const) имеет вид

const, (2.40)

где f - площадь рассматриваемого сечения канала; ρ, v и w - плотность, удельный объем и скорость рабочего тела в этом сечении канала.

Если формулу (2.40) последовательно прологарифмировать и продифференцировать, получим уравнение неразрывности потока в дифференциальной форме

. (2.41)

Течение рабочего тела через канал (см.рис. 2.10) предполагается адиабатным . Это допущение объясняется ничтожной малостью тепловых потерь через стенки канала по сравнению с количеством теплоты, протекающей по каналу вместе с потоком рабочего тела. В данном случае справедливо применение уравнения адиабаты

const. (2.42)

Осуществляя процедуру логарифмирования и дифференцирования над этой зависимостью, находим

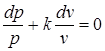. (2.43)

Рассматривая совместно выражения (2.41 и 2.43) и используя уравнение (2.39), получаем

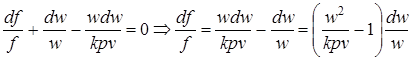. (2.44)

Введя обозначения , , 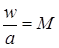где а представляет скорость звука и M - число Маха, получаем уравнение неразрывности в виде

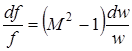. (2.45)

Последнее уравнение учитывает зависимость скорости потока w от геометрической формы канала f и представляет математическую запись закона геометрического обращения воздействия.

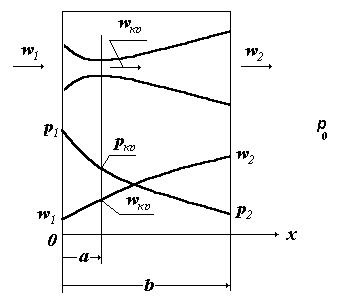
Рис. 2.11

Характерные возможные случаи движения рабочего тела в каналах переменного сечения:

а) при М <1, если по ходу движения поток сужается (df<0), то скорость растет (dw>0), а при расширении канала (df>0), скорость потока уменьшается (dw<0);

б) при М>1 имеют место следующие случаи:

для df>0, dw>0;

для df<0, dw<0.

На рис. 2.11 представлен канал переменного сечения, который состоит из сужающегося участка (0<x≤а) и расширяющегося участка (а<х≤b). Подобным образом совмещенный канал носит название сопла Лаваля, который служит для получения сверхзвуковых скоростей.

Иллюстрированная на рис. 2.11 картина распределения давления и скорости потока вдоль сопла соответствует так называемому расчетному режиму работы сопла Лаваля. Этот режим имеет место при р₂=р_о, где р_о – давление окружающей среды и при условии, что в минимальном сечении сопла достигнута скорость потока, равной местной скорости звука.

При условии р₂ ≠ р_о – режимы течения газа и сопло Лаваля называются нерасчетными.

При р₂ > р_о – сопло называется недорасширенным;

При р₂ < р_о – перерасширенным.

При соблюдении условий расчетного режима сопло Лаваля позволяет получить сверхзвуковую скорость истечения. Конкретная сверхзвуковая скорость истечения зависит от значений параметров: р₁ и Т₁ – давления и температуры во входном сечении, 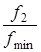- отношения площадей выходного и минимального сечений сопла, а также от давления окружающей среды р_о.

Следует отметить, что для того чтобы получить другую сверхзвуковую скорость истечения, не меняя параметров газа на входе в сопло р₁, Т₁, необходимо воспользоваться другим соплом с другим отношением выходного сопла к минимальному .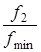

Очевидно, что если в минимальном сечении сопла не достигнута критическая скорость потока, то на всем протяжении сопла Лаваля будет дозвуковой режим движения, следовательно, скорость истечения из сопла также будет дозвуковая.

Дата добавления: 2014-12-07