Решение. Необходимо определить v1, v2, v3, v4, p2, p3, p4, t2, t3, t4, ηt, lц

Дано: p₁, t₁, , | q₂ |.

Необходимо определить v₁, v₂, v₃, v₄, p₂, p₃, p₄, t₂, t₃, t₄, η_t, l_ц.

1. Представим рассматриваемый цикл в координатах p, v и T, s, следуя рис. 4.2.

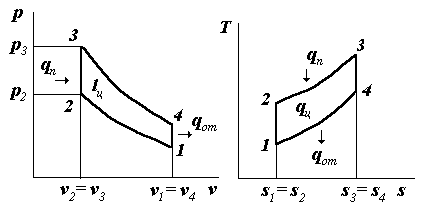
Рис. 4.2

Параметры точки 1: p₁ =0,1·10⁶ Па; T₁ =273+ t₁ =293 К.

Удельный объем определяем с помощью формулы (1.4).

.

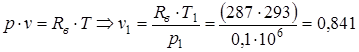Параметры точки 2: находим, исследуя адиабатный процесс 1-2, который описывается формулой (1.59):

.

В соответствии с формулой (1.60)

,

.

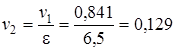Для нахождения параметров точек 3, 4 составляем зависимости, соответствующие процессам: 2-3; 3-4; 4-1. Процесс 2-3 - изохорный, v₃=v₂= const. Из уравнения состояния pv=R_в·T следует const. Следовательно,

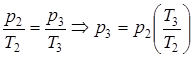. (4.4)

Для изохорного подвода теплоты справедлива зависимость

q₁=с_v· (T₃-T₂). (4.5)

Процесс 3-4 - адиабатный:

p₃ =p₄ . (4.6)

Процесс 4-1 - изохорный:

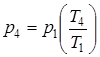; (4.7)

и изохорный отвод теплоты

q₂=с_v ·(T₄–T₁). (4.8)

В уравнениях (4.4 – 4.8) неизвестными являются p₃, T₃, p₄, T₄, q₁. Решая эту замкнутую систему уравнений, находим искомые величины:

,

,

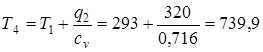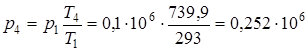p₃ = p₄·ε^k =0,252·10⁶·6,5^1,4=3,46·10⁶,

.

Параметры всех характерных точек найдены.

Находим количество подведенной теплоты в соответствии с формулами:

q₁ = c_v (T₃-T₂)=0,716 (1559-619)=673.

Определяем термический КПД по формуле (3.16):

.

Рассчитываем работу цикла l_ц = q₁-q₂ =(673-320)=353 кДж/кг.

Находим термический КПД цикла Карно в диапазоне температур

= T₃ =1559 K, = T₁ =293.

.

Пример 3. Из сужающегося сопла вытекает кислород, находящийся в резервуаре, давление и температура в котором р ₁=6 МПа, t₁ =100^оС. Давление среды, в которую проходит истечение р₂ =3,6 МПа.

Определить скорость истечения и расход кислорода, если площадь выходного сечения f =20 мм².

Газ подчиняется уравнению Клапейрона - Менделеева pv=RT, теплоемкость не зависит от температуры. Входная скорость кислорода близка к нулю. Процесс изменения состояния текущего газа изоэнтропный.

Решение. Прежде всего, устанавливаем каков режим истечения, для чего находим значение параметра .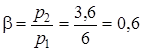

Сравниваем полученное значение с критическим отношением давлений в соответствии с формулой (2.56).

,

где k =1,4 - коэффициент адиабаты;

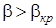, т.е. это означает, что давление среды перед соплом больше, чем критическое, следовательно, располагаемый перепад давления будет использован полностью для разгона потока газа.

На выходе из сопла установится давление, равное давлению среды, а скорость истечения окажется меньше критической скорости, т.е. режим истечения будет - дозвуковой.

Определяем скорость истечения в соответствии с формулой (2.52):

.

Подсчитываем удельный объем кислорода на выходе из сопла:

.

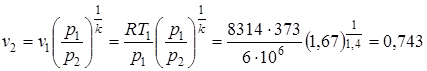В заключение находим массовый расход кислорода при помощи уравнения неразрывности (2.40):

.

Пример 4. Необходимо определить конструктивные параметры сопла Лаваля, которое должно работать при следующих условиях.

На входе сопла давление и температура воздуха соответственно
р₁ =0,9 МПа, Т₁ =1100 К, в выходном сечении давление р ₂=0,11 МПа. Массовый расход газа G =0,7 кг/с.

Истечение через сопло адиабатное, при k =1,4. Трение газа в каннале и входная скорость его не учитываются. Удельная газовая постоянная
R =287 Дж/(кг∙К).

Решение. Находим отношение давлений в выходном сечении сопла:

.

По формуле (2.56) определяем критическое значение :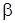

.

Для условий данного примера имеет место условие 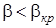, следовательно, в минимальном сечении сопла будет достигнута критическая скорость и сопло Лаваля будет работать в сверхзвуковом режиме. Критическую скорость, соответствующую начальной температуре Т₁ =1100 К, определяем по формуле (2.57)

.

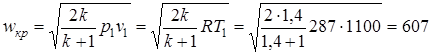Площадь минимального сечения сопла находим по формуле:

,

где ; .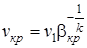

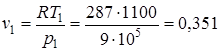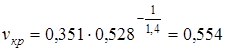м³/кг; .

Диаметр минимального сечения сопла

.

Длину сужающейся части сопла l₁ обычно принимают равной диаметру минимального сечения:

l₁ =29.

Скорость газов в выходном сечении сопла находим по формуле (2.52):

.

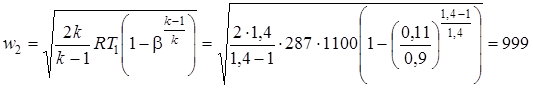Площадь выходного сечения сопла находим по формуле

,

где м³/кг.

Диаметр выходного сечения будет равен

.

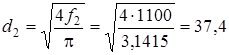Длину расходящейся части сопла l₂ находим по формуле (2.60), приняв угол конусности равным .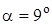

.

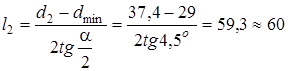Пример 5. Определите состояние пара за турбиной и подсчитайте внутренний КПД паротурбинной установки, если начальные параметры р₁=13,0 МПа и t₁=565 °С, давление в конденсаторе р₂=40 гПа, внутренние относительные КПД турбины и питательного насоса соответственно 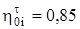и .

Решение. Цикл, по которому работает установка, изображен на рис. 35.

Сначала определим состояние пара в конце изоэнтропного расширения пара в турбине. Начальную энтальпию и энтропию находим по таблицам [7]:

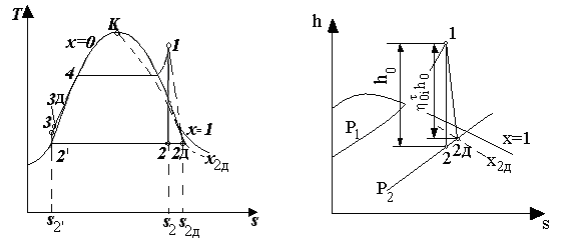
а б

Рис. 4.3

Для р₁ = 13,0 МПа и t₁ = 565 °С, 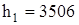кДж/кг и кДж/(кг·К). Для р₂ = 40 гПа: определяем 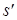= 0,4225 кДж/(кг·К), = 8,473 кДж/(кг·К), r = 2433 кДж/(кг·К), =121 кДж/(кг·К). Энтальпию пара в точке 2 находим, рассчитывая изоэнтропный процесс 1-2:

кДж/кг.

Таким образом, изоэнтропный теплоперепад

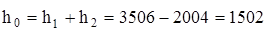кДж/кг.

По определению

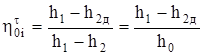
Следовательно,

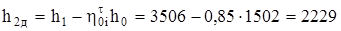кДж/кг.

Зная энтальпию, легко найти остальные параметры при р₂=40 гПа. Для этого сначала необходимо найти степень сухости в конце действительного процесса расширения:

.

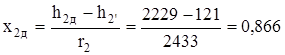Внутренний КПД цикла определяется по формуле

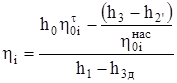
Находим энтальпию воды после теоретического и действительного (с учетом потерь) сжатия в насосе. Энтальпия кДж/кг, энтропия 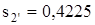кДж/(кг·К). Энтальпия в точке 3 определяется в результате изоэнтропного процесса 2-3 ( ). Интерполируя табличные данные [7], находим при давлении р₃=р₁=13,0 МПа и s₃=0,4225 кДж/(кг·К) энтальпию h₃=134,8 кДж/кг. Разность h₃-h_2’=134,8-121,4=13,4 кДж/кг представляет собой теоретическую работу насоса.

Вычислим энтальпию в конце сжатия h_3д с учетом потерь

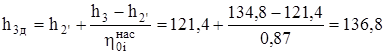кДж/кг.

Таким образом,

.

Определяем термический КПД цикла Ренкина (который не учитывает потери):

.

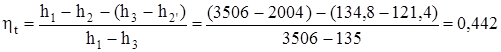Если при определении внутреннего КПД установки пренебречь работой насоса, то окажется, что

.

Здесь 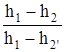= есть несколько завышенный термический КПД цикла не учитывающий работу насоса.

Разница и 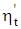в нашем случае составляет 0,45 %. Приблизительно такой же будет ошибка и в определении расхода топлива. Тем не менее, соотношение

широко применяется в теплотехнических расчетах. Его можно считать вполне удовлетворительным при невысоких параметрах пара перед турбиной, когда работой насоса можно пренебрегать.

Пример 6. Паротурбинная установка, оснащенная теплообменниками смешивающего типа, работает по регенеративному циклу, имея два отбора при давлениях р_m =1 МПа; р_n =0,1 МПа. Турбина работает с начальными параметрами пара р₁ =5 МПа, t₁ =400^oC, а давление в конденсаторе р₂ =5 кПа.

Определить термический КПД для регенеративного цикла Ренкина , удельный расход пара сравнить с КПД цикла Ренкина без регенеративного подогрева питательной воды.

Дата добавления: 2014-12-07