Определение линейных скоростей точек звеньев и угловых скоростей звеньев

При выполнении кинематического анализа механизма выбирается последовательно одно из положений механизма, для которого осуществляется следующие операции:

- составляются векторные уравнения для определения скоростей точек

звеньев механизма;

- записываются выражения для определения угловых скоростей

звеньев;

- задается масштаб плана скоростей;

- строится в заданном масштабе план скоростей;

- определяются величина и направление угловых скоростей звеньев;

Такие же операции выполняются для определения ускорений точек звеньев. Кинематический анализ выполним на примере одного из положений рассмотренного выше кривошипно-ползунного механизма (рисунок 2.2)

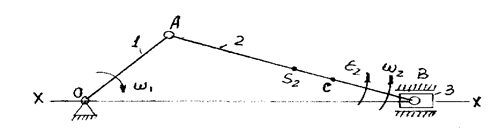
Рисунок 2.2 − Схема положения звеньев механизма

1. Составляем векторные уравнения скоростей точек звеньев.

V_A =w₁·OA, где V_A ┴ OA, (2.1)

V_В = V_А + V_ВА, где V_B ║ X-X, V_BA ┴ BA, (2.2) Примечание: Векторные величины в уравнениях здесь и далее будем обозначать жирным шрифтом, скалярные – обычным.

В уравнении (1) скорость т. А известна по направлению, а величину легко определить по заданным значениям угловой скорости ω, и длине начального звена ОА. Движение т. В в уравнении (2) можно разложить на переносно-поступательное со скоростью т. А и относительно-вращательное вокруг т. А. Не известные величины векторов скоростей V_B и V_BA, могут быть определены построением плана скоростей.

Для этого в качестве полюса плана скоростей выбираем точку p,откладываем от нее отрезок pа, предоставляющий собой скорость точки А в каком-либо произвольно выбранном масштабе, например, μ = V_A/ ра м/с/мм.

При построении плана скоростей отрезок pа откладываем перпендикулярно вектору V_A и, далее, от конца вектора pа откладываем отрезок ва, перпендикулярно вектору V_BA и отрезок рв, параллельно оси Х-Х (рисунок 2.3).

Для определения истинных величин скорости V_B и V_BA, достаточно измеренные на плане отрезки рв и ва умножить на масштаб μ, получим

V_B = μ · рв, V_BA = μ · ва, (2.3)

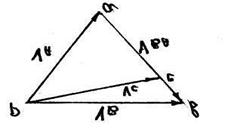
Рисунок 2.3 − План скоростей

Из плана скоростей можно определить скорость любой точки на звене (например, т. С на звене 2). Для этого необходимо использовать теорему подобия и составить пропорцию

СВ/АВ = св/ав, откуда св =ав ∙СВ/АВ, (2.4)

где СВ и АВ длины участков звеньев механизма.

Соединив полюс р с точкой с на плане скоростей, получим вектор, изображающий скорость точки с

тогда V_C = рс ·μ, (2.5)

Для определения направления и величины угловой скорости звена 2 воспользуемся известным соотношением

V_BA =w₂ ·BA, (2.6)

откуда w_{2 =} V_BA/ BA, (2.7)

Направление угловой скорости совпадает с направлением вектора V_{BA .} Проставляем направление w₂ на звене 2 стрелкой.

Дата добавления: 2014-12-07