Силовой анализ механизма

Задачей силового анализа (расчёта) является:

- определение реакций в кинематических парах механизма по известным внеш-ним силам.

- определение уравновешивающей силы, приложенной к начальному звену в т. А

- подбор мощности двигателя по уравновешивающей силе.

Силовой анализ (расчёт) механизма выполним на рассмотренном ранее простейшем кривошипно-ползунном механизме. Для этого вычертим в одном из положений механизм и приложим действующие на звенья внешние силы (рисунок 3.2).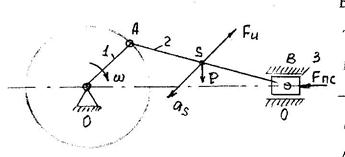

Рисунок 3.2 − Схема кривошипно-ползунного механизма

Силовой анализ начинается с последней присоединённой группы Ассура и заканчивается начальным звеном.

Этот механизм, как было выявлено ранее, состоит из группы Ассура

2-го класса, 2 порядка (звенья 2, 3) и механизма 1-го класса (звенья 0, 1).

Будем считать звенья 1, 3 невесомыми, тогда на звено 2 будут действовать внешняя сила инерции Fu и сила тяжести P, а на звено 3 – сила полезного сопротивления F_пс, (для ДВС − движущая сила) и реакции кинематических парах 0, 3; 1, 2.

Для определения реакций в кинематических парах 0, 3; 1, 2 вычерчиваем последнюю присоединенную группу Ассура (рисунок 3.4) и расставляем все внутренние и внешние силы, заменив действие звена 0 на звено 3 реакцией 0, 3, а действие звена 1 на звено 2 нормальной и тангенциальной реакциями F ^τ 12 и F ⁿ 12.

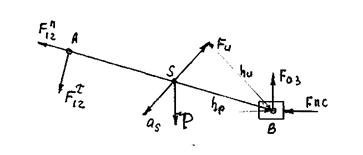Под действием этих сил звенья находятся в равновесии.

Рисунок 3.3 − Схема приложения внешних и внутренних сил к гр. Ассура

Составим уравнение равновесия группы Ассура

F^τ ₁₂ + Fⁿ₁₂ + Fu + P + F₀₃ + Fnc = 0 (3.7)

Известными в данном уравнении являются внешние силы Fu, P, и Fnc, неизвестными F^τ 12, Fⁿ12 и F03. Тангенциальную составляющую F^τ 12 можно найти из условия равновесия моментов

∑MB = 0 F^τ₁₂ · AB + P · hp –F_иh_u = 0 (3.8)

откуда

F^τ ₁₂ = Fu · h_u – Ph_p /AB (3.9)

Если получим результат со знаком «-» направление F^τ ₁₂ следует поменять на противоположное.

Неизвестные Fⁿ₁₂ и F₀₃ определим построением плана сил. Для этого зададимся масштабом сил. Пусть

µ = P / l (3.10)

где l – отрезок произвольной длины 50…100мм, соответствующий в масштабе силе Р.

Используя масштаб, найдём длины отрезков соответствующие внешним силам.

l Fпс = Fnc / µ, (3.11)

l _Fu = Fu / µ, (3.12)

l _F^τ ₁₂ = F^τ 12 / µ. (3.13)

Построение плана сил целесообразно начинать с одной из неизвестных сил Fⁿ12 или F03.

Выберем, например, силу Fⁿ1,2. Так как длина отрезка, изображающая силу неизвестна, проведем произвольной длины линию, параллельную направлению силы Fⁿ₁₂.

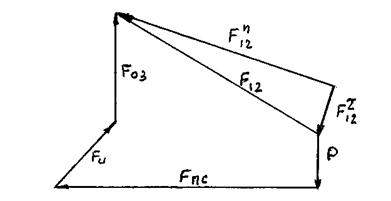От этой линии с любого её конца откладываем последовательно отрезки l _F^τ_12,, l _F, l _P, l _Fu. Последним откладываем отрезок (проводим линию) параллельный другой неизвестной силе F03. Силовой многоугольник замкнётся. Результирующей всех сил будет сила F₁₂. (рисунок 3.5).

Рисунок 3.5 − План сил группы Ассура (звенья 2, 3).

Измерив длину отрезков l _Fⁿ₁₂, l _F12, l F₀₃, и, умножив их на масштаб, получим численное значение этих сил (рисунок 3.5).

Fⁿ₁₂ = l _Fⁿ₁₂ ∙ µ, (14)

F₁₂ =l _F12 ∙µ, (15)

F₀₃ = l _F03 ∙ µ. (16)

Рассмотрим теперь начальное звено. Вычертим начальное звено и стойку (звенья 0, 1 − рисунок 3.6). Для его уравновешивания необходимо ввести дополнительную силу, уравновешивающую все приложенные к начальному звену силы. Обозначим её через Fyр и приложим к т. А звена 1.

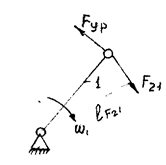
Рисунок 3.6 − Схема начального звена

Как видно из силового многоугольника (рисунок 3.5) результирующей всех сил, действующих на звенья 2, 3, является сила F₁₂ приложенная к т..

Приложим к начальному звену все внешние и внутренние силы, при этом вместо результирующей силы F₁₂, прикладываем равную ей по величине, но противоположно направленную силу F₂₁ . Такими силами будут F_yр; F₂₁; F₀₁. Составим уравнение равновесия этих сил

Fyp + F₂₁+ F₀₁ =0. (3.17)

Неизвестную Fyp можно найти из уравнения равновесия моментов

Mo (F₂₁) = M (Fyp) = 0, (3.18)

или F₂₁ ∙ l₂₁ – Fyp ∙ OA = 0, (3.19)

откуда Fyp = F₂₁ ∙ l₂₁/OA, (3.20)

Длину отрезка уравновешивающей силы найдем из соотношения

l _Fyp = Fуp / µ, (3.21)

Построив план сил можно найти другую неизвестную силу F01. (рисунок 3.7)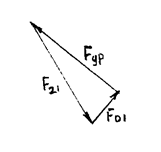

Рисунок 3.7 − План сил начального звена

Измерив длину отрезка F01 и, умножив её на масштаб, получим реакцию F01.

F₀₁ = l_F01 ∙ µ. (3.22)

По величине уравновешивающей силы можно определить необходимую мощность двигателя, приводящую весь механизм в движение.

4. Приведённые силы

При исследовании движения механизма, находящегося под действием заданных сил, удобно все силы, действующие на звенья, заменить силами, приложенными к одному из звеньев. При этом необходимо, чтобы робота на рассматриваемом возможном перемещении или мощность, развиваемая заменяющими силами, были соответственно равны сумме робот или мощностей, развиваемых силами, приложенными к звеньям исследуемых механизмов. Удовлетворяющие этим условиям силы называются − приведёнными силами.

Звено, к которому приложены приведённые силы, называется – звеномприведения, а точка приложения сил – точкой приведения. Обычно за звено приведения принимают начальное звено (рисунок 3.8).

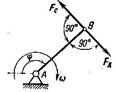
Рисунок 3.8 − Схема звена приведения

К точке В приложены две силы:

- F_д – приведённая движущая сила,

- F_с – приведённая сила сопротивления.

Движущая сила F_д должна производить роботу, равную работе всех движущих сил, а сила сопротивления F_с – работе всех сил сопротивления.

Дата добавления: 2014-12-07