Виды зубчатых передач и зубчатых колес

План

Лекция № 7 Зубчатые передачи

1. Виды зубчатых передач и зубчатых колес.

2. Геометрические соотношения в эвольвентном зубчатом зацеплении.

3. Косозубые и шевронные колеса.

4. Силы, действующие в зацеплении.

5. Методы изготовление и материалы зубчатых колес.

Зубчатые передачи широко применяются во всех отраслях машиностроения и приборостроения. В них движение передается с помощью зацепления пары зубьев колес находящихся на ведущем и ведомом валах.

В зависимости от относительного положения геометрических осей ведущего и ведомого вала различают:

- зубчатые передачи с цилиндрическими колесами (оси параллельны),

- передачи с колесами коническими (оси пересекаются),

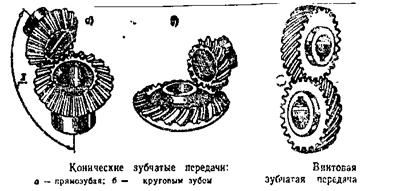
- передачи с винтовыми и гипоидными колесами (рисунок 7.1), а также червячные (оси скрещиваются).

По расположению зубьев относительно образующей зубчатые колеса бывают:

- прямозубые;

- косозубые;

- шевронные.

Рисунок 7.1 – Виды зубчатых передач

Зубья колес могут быть: прямые, косые, криволинейные. Цилиндрические зубчатые колеса могут быть с внешним и внутренним зацеплением.

По конструктивному исполнению зубчатые передачи делятся на открытые и закрытые.

Зубчатое колесо передачи с меньшим числом зубьев называется шестерней, а с большим − колесом. При одинаковом числе зубьев шестерней является ведущее колесо.

Передаточное отношение зубчатых колес выражается формулой

U =± ω₁ / ω₂, (7.1)

где ω₁ - угловая скорость ведущего колеса, а ω₂, − ведомого.

Знак «−» указывает на противоположное направление вращения колес (внешнее зацепление рисунок 2 а, б), знак «+»− на одинаковое направление вращения колес (внутреннее зацепление).

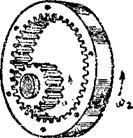
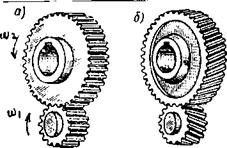
Рисунок 7.2 − Виды зацепления зубчатых колес

Достоинства зубчатых передач:

- высокий КПД;

- компактность;

- надежность работы;

- простота эксплуатации;

- постоянство передаточного отношения;

- большой диапазон передаваемых мощностей (от 0,001 до десятков
тысяч КВт).

Недостатки:

- сложность изготовления;

- шум при неточном изготовлении и высоких скоростях вращения.

Кривые, которыми очерчены профили зубьев, должны обеспечивать постоянство передаточного отношения. Для этого необходимо, чтобы выполнялся основной закон зацепления:

Для сохранения постоянства передаточного отношения необходимо и достаточно, чтобы нормаль NN к профилю зубьев в точке их соприкосновения всегда пересекала линию центров О₁О₂ в одной и той же точке Р₀, называемой полюсом. Эта точка делит линию центров О₁О₂ в отношении равном передаточному числу (рисунок 7.3).

U = ω₁ / ω₂ = R₂ / R₁, (7.2)

Рисунок 7.3 – Схема к основному закону зацепления

Этому закону соответствует множество кривых, но чаще всего используется эвольвентная кривая.

Линия NN называется линией зацепления. Угол между линией зацепления и касательной к делительным окружностям называется углом зацепления α.

При изготовлении колес с малым числом зубьев может происходить подрезание зубьев у основания зуба (рисунок 7.4), что значительно снижает его прочность. Поэтому принимают минимальное число зубьев равное 17, при нормальной высоте зубьев и 14 при укороченных зубьях.

Рисунок 7.4 – Подрезание зубьев

Для устранения подрезания зубьев при нарезании их с помощью инструментальной рейки ее отодвигают на величину

b=x∙m, (7.3)

где m = p/ π - модуль зубьев;

р -окружной шаг зубчатого зацепления;

х - коэффициент сдвига, который рассчитывается по формуле

x = (17 - Z_min) /17, (7.4)

Z_min – минимальное число зубьев, при котором их подрезание отсутствует.

Дата добавления: 2014-12-07