Поліноміальна апроксимація

Логарифмічна апроксимація

Логарифмічна апроксимація добре описує величину, яка спочатку швидко росте або убуває, а потім поступово стабілізується. Описує як позитивні, так і негативні величини.

Формула:

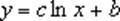
де з і b - константи, ln - функція натурального логарифма.

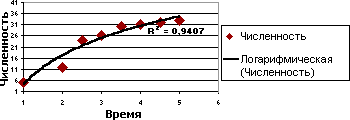
Приведений вище приклад використовує логарифмічне наближення для ілюстрації прогнозованого зростання популяції тварин на обмеженій території. У міру того, як вільного простору стає все менше, темпи зростання популяції також знижуються. Слід відмітити, що значення R² в даному прикладі рівне 0,9407; це указує на те, що апроксимуюча крива описує дані з достатньо високою мірою достовірності.

Поліноміальна апроксимація використовується для опису величин, що поперемінно зростають і убувають. Вона корисна, наприклад, для аналізу великого набору даних про нестабільну величину. Ступінь полінома визначається кількістю екстремумів (максимумів і мінімумів) кривої. Поліном другого ступеня може описати тільки один максимум або мінімум. Поліном третього ступеня має один або два екстремуми. Поліном четвертого ступеня може мати не більш три екстремуми.

Формула:

де b і — константи.

Нижче на прикладі апроксимації поліномом другого порядку (одна вершина) показана залежність швидкості від споживання палива. Слід відмітити, що значення R² в даному випадку складає 0,9474. Це досить добре узгоджується з фактичними даними.

Дата добавления: 2014-12-07