Експоненціальна апроксимація

Степенева апроксимація

Степеневе наближення дає добрі результати, якщо залежність, яка міститься в даних, характеризується постійною швидкістю росту. Прикладом такої залежності може служити графік прискорення автомобіля. Якщо в даних є нульові або негативні значення, використовування степеневого наближення неможливе.

Формула:

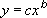
де з і b - константи.

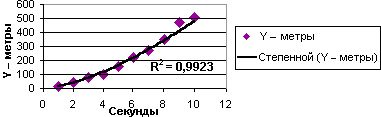
Нижче показаний приклад залежності пройденої відстані від часу (у секундах). По степеневій лінії тренда ясно видно збільшення прискорення. Зверніть увагу, що значення R² в даному прикладі рівне 0,9923. Це говорить про високу точність використовуваного наближення.

Експоненціальне наближення слід використовувати в тому випадку, якщо швидкість зміни даних безперервно зростає. Однак для даних, які містять нульові або негативні значення, цей вид наближення непридатний.

Формула:

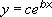
де з і b - константи, e - основа натурального логарифма.

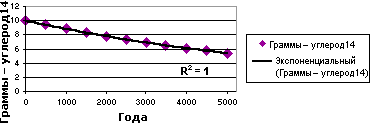
На приведеному нижче прикладі експоненціальне наближення ілюструє процес розпаду вуглецю 14. Слід відмітити, що значення R² тут рівне 1, тобто лінія наближення ідеально відповідає даним.

Ковзаюче середнє (лінійна фільтрація)

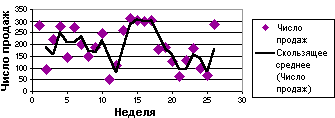
Використовування як наближення ковзаючого середнього дозволяє згладити коливання даних і таким чином наглядніше показати характер залежності. Така лінія тренда будується по певному числу точок (воно задається параметром Шаг). Елементи даних усереднюються, і одержаний результат використовується як середнє значення для наближення. Так, якщо Шаг рівний 2, перша точка згладжуючої кривої визначається як середнє значення перших двох елементів даних, друга точка — як середнє наступних двох елементів і так далі. Для ковзаючого середнього значення R² не може бути відображене.

Формула:

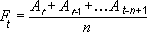
У наступному прикладі показана залежність числа продажів впродовж 26 тижнів, одержана шляхом розрахунку ковзаючого середнього.

Дата добавления: 2014-12-07