Уравнение Бернулли

В некоторых задачах о движении жидкости в приближении рассматривается идеальная (невязкая) жидкость.

Уравнение Бернулли для потока идеальной жидкости представляет закон сохранения энергии жидкости вдоль потока: вдоль элементарной струйки идеальной жидкости сумма потенциальной и кинетической энергии является постоянной величиной, т.е.

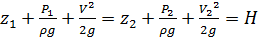, (5.1)

где Н - полный гидродинамический напор (полная удельная энергия жидкости в сечении); Z – вертикальная координата центров тяжести сечений (геометрический напор); 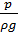– пьезометрический напор (удельная энергия давления); 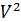/2g – скоростной напор (удельная кинетическая энергия), сумма 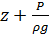представляет собой потенциальную энергию.

В реальных жидкостях проявляется влияние сил внутреннего трения, обусловленных вязкостью, на преодоление которых расходуется определенное количество кинетической энергии или скоростного напора h.

Уравнение Бернулли для двух сечений потока реальной жидкости записывается в следующем виде

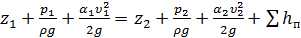(5.2)

где υ - средняя по сечению скорость; α – коэффициент Кориолиса, учитывающий неравномерность распределения скоростей по сечениям (при турбулентном режиме движения жидкости α =1, при ламинарном - α =2).

Член выражает потери напора на преодоление различных сопротивлений на пути движения жидкости между рассматриваемыми сечениями потока:

1) Сопротивления по всей длине потока жидкости, вызванное силами трения частичек жидкости между соседними слоями жидкости и трением о стенки, ограничивающие поток.

Потери напора называют линейными - .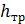

2) Сопротивления, обусловленные местными препятствиями, встречающимися на пути движения (изменение формы и размеров русла). Они ведут к изменению величины и направления скорости.

Потери напора называют местными - .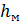

Таким образом, гидродинамический напор в первом сечении всегда больше гидродинамического напора во втором сечении на величину потерь .

Дата добавления: 2014-12-07