Гидравлический расчет трубопроводов

Все трубопроводы подразделяются на две категории: простые и сложные. Простой трубопровод не имеет разветвлений на пути движения жидкости, но может представлять последовательное соединение труб разного диаметра. Сложный трубопровод имеет хотя бы одно разветвление и может содержать как параллельные и последовательные соединения труб.

Если в трубопроводе необходимо обеспечить расход жидкости Q, то потребный для этого напор Н _потр. – пьезометрическая высота в начальном сечении определяется по формуле

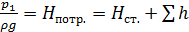, (6.1)

где 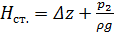– статический напор, 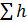- суммарные потери напора на сопротивление в трубопроводе.

Суммарная потеря напора складывается из потерь на трение по всей длине трубы и местных потерь

= +

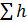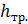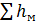
Для определения потерь напора на трение в трубах круглого сечения можно использовать формулу Дарси, которую для дальнейших расчетов удобно выразить через расход:

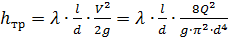(6.2)

где l – длина рассматриваемого участка трубопровода; d – диаметр трубопровода; λ – безразмерный коэффициент гидравлического трения (коэффициент Дарси).

При турбулентном движении коэффициент трениязависит от числа Рейнольдса 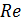и относительной шероховатости трубы ε 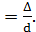Значения эквивалентной (абсолютной) шероховатости Δ для различных труб представлены в Приложении 7.

Универсальной формулой, учитывающей одновременно оба фактора является формула Альтшуля:

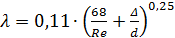(6.3)

Для гидравлически гладких труб шероховатость на сопротивление не влияет, и коэффициент сопротивления 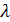однозначно определяется числом Рейнольдса:

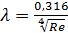(6.4)

Местные потери напора определяются по формуле Вейсбаха:

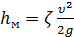(6.5)

где υ – средняя скорость потока в сечении перед местным сопротивлением ζ – коэффициент местного сопротивления (определяется формой местного сопротивления и его геометрическими параметрами).

C учетом формул Дарси и Вейсбаха,

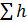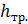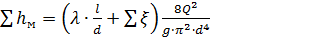= + (6.6)

При внезапном расширении трубы потеря напора происходит при вводе жидкости в силовые цилиндры, пневмогидравлические аккумуляторы, фильтры и прочие устройства. Величина этой потери равна скоростному напору потерянной скорости (теорема Борда):

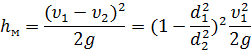
Обозначим 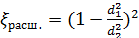- коэффициент местных сопротивлений при расширении трубы, где d₁ и d ₂ – внутренние диаметры сечений трубы перед и за расширением.

В случае внезапного сужения трубопровода коэффициент местных сопротивлений равен

,

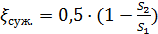где S₁ и S ₂ – площади сечений трубы до и после сужения.

Формула (6.6) справедлива для обоих режимов, однако для ламинарного режима удобнее использовать формулу Пуазейля:

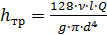, (6.7)

в которой необходимо заменить фактическую длину трубопровода расчетной, равной

,

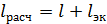где 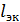– длина, эквивалентная всем местным гидравлическим сопротивлениям в трубопроводе.

Формула для расчета потребного напора имеет вид

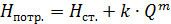, (6.8)

где для ламинарного режима течения

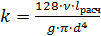, m =1; (6.9)

турбулентного режима течения

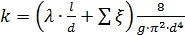, m =2 (6.10)

Характеристики потребного напора 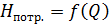и суммарных потерь напора трубопроводов 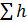= 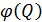при ламинарном режиме представляет прямые, при турбулентном - параболы.

Дата добавления: 2014-12-07