Кіріспе 2 страница

Өлшеуіш – физикалық шаманың берілген өлшемін жаңғырту үшін тағайындалған ӨҚ. Өлшеу кезінде классификациялық белгісі өлшеуіштің бары немесе жоғы болып табылады.

Тікелей баға беру әдісі (ТББӘ) – өлшеуіштің жоғы – шама мәнін тура әсер ететін өлшеу аспабының санауыш құрылғысы арқылы тікелей анықтайтын өлшеу әдісі.

Мысалы: серпінді таразысында салмақты өлшеу, t⁰ – термометрмен.

Сызықтық өлшеулердің дәлдігін көтеру үшін шкала және нониус (қосымша шкала) арқылы санау әдісі қолданылады. Бұл әдіс шкалалардың (негізгі және қосымша) белгілерінің түйіскенін қолдануымен сипатталынады.

Өлшеуішпен салыстыру әдісі ( ӨСӘ ) – бұл өлшеу әдісі өлшенетін шаманы өлшеуішті жаңғырту шамасымен салыстыруына негізделген.

Өлшенетін шама және өлшеуішті жаңғырту шамасы арасында айырмашылығы бар немесе жоқ болуына қарай нөлдік және дифференциалдық әдістерін айырады.

Нөлдік әдіс – бұл ӨСӘ, мұнда салыстыру аспабына әсер етуші нәтижелік эффектін нөлге дейін жеткізеді. Мысалы, иықтары тепе-тең таразымен салмақты өлшеу, бұл кезде салмақ массасы салмақты теңестіретін гир массасымен анықталады.

Дифференциалды әдіс – бұл ӨСӘ, мұнда өлшеу аспабына өлшенетін және белгілі өлшеуішпен жаңғыртатын шамалардың айырымы әсер етеді. Айырым өлшенеді. Мысалы, иықтары тепе-тең меңзерлік таразымен салмақты өлшеу, бұл кезде салмақтың және гирдің таразы серіппесіне әсерлері толық емес, қарама-қарсы қойылады, айырымы аспап шкаласында меңзермен белгіленеді:

а) қарама-қарсы қою әдісі - бұл ӨСӘ, мұнда өлшенетін және өлшеуішпен жаңғыртатын шамалар бір мезгілде салыстыру аспабына әсер етеді, соның көмегімен осы шамалардың арақатынасы жойылады;

б) ауыстыру әдісі - бұл ӨСӘ, мұнда өлшенетін шама белгілі өлшеуішпен жаңғыртатын шамамен ауыстырылады;

в) түйісу әдісі – бұл ӨСӘ, мұнда өлшенетін және өлшеуішпен жаңғыртатын шамалардың айырымын өлшеу үшін шкала белгілерінің немесе периодикалық сигналдардың түйісуі қолданылады.

Дифференциалды әдісін қолдану үшін өлшенетін шамаға жақын жоғары дәлдік өлшеуіш болуы керек.

Тақырып бойынша қосымша ақпаратты [1-6,8,9] әдебиеттен алуға болады.

3 дәріс. Өлшеулер қателігі

Дәрістің мазмұны: өлшеулер қателігінің классификациясы; кездейсоқ және жүйелік қателігі; кездейсоқ шаманың таралу заңдары.

Дәрістің мақсаты: әртүрлі өлшеулер қателіктердің негізгі анықтамаларын оқу, кездейсоқ шаманың таралу заңдарының негізгі мінездемелері, байқау қатарының негізгі мінездемелерін бағалау.

Пайда болу себептеріне, өзгеру мінезіне және көрініс жағдайына байланысты өлшеулер қателіктерінің классификациясы В қосымшасында В.1 суретте келтірілген.

Олардың көрініс мінезіне тәуелді қателіктерді кездейсоқ және жүйелікдеп ажыратады.

Кездейсоқ қателіктері – бұл қателіктер бір шаманы қайталап өлшеген кезде кездейсоқ түрде өзгереді.

Кездейсоқ қателіктерінің мәнін және таңбасын анықтау мүмкін емес. Кездейсоқ қателіктерін есептеу үшін қат-қабат (статистикалық) өлшеулер жасалынады. Кездейсоқ қателіктерін бағалағанда күтетін қателікті айтады. Өрескел қателік – бұл кездейсоқ қателік. Мүлт жіберу – бұл қателік өлшеу нәтижесін ашықтан-ашық бұрмалайды. Эксперимент жасайтын адамның кездейсоқ субъективті қателігі мүлт жіберу деп алынады. Өрескел қателіктер және мүлт жіберу, әдетте, байқау нәтижелерінің статистикалық өңдеуі басталғанша экспериментальдік деректерден жойылады.

Жүйелік қателік – бір және сол шаманы қайталап өлшеулерде тұрақты немесе заңды өзгеретін болып қалатын қателік өлшеуі.

Егер жүйелік қателік белгілі болса, яғни белгілі мәні және таңбасы болса, онда ол өлшеудің аяқталуы бойынша түзету енгізу жолымен алынып тасталуы мүмкін. Егер жүйелік қателіктің себебі (көзі) белгілі болса, онда оны өлшеуге дейін шығарып тастау қажет.

Жүйелік қателіктердің туу салдарына байланысты өлшеу әдісі қателігі, құралдық қателік, орнату қателігі, субьективті қателік, әдістемелік қателік болып бөлінеді.

Өлшеу әдісі қателігі (теориялық қателік) – бұл өлшеу әдісінің жетімсіздік қателігі. Негізінде бұл өлшеу принципінің жетімсіздігі өлшеу негізіне алынған құбылыстың жеткілікті зерттелмеуі.

Құралдық қателік (құралдың қателігі) - қолданылатын өлшеу құралдарының қателіктеріне байланысты туатын қателіктер (конструкцияның, өлшеу құралдарының жасалу технологиясының жетімсіздігі, олардың бірте-бірте тозуы, материалдардың ескіруі).

Орнату қателігі - өлшеу құралдарын дұрыс орнатпау қателіктері. Әдістемелік қателік – шаманы өлшеу әдістемесінде жіберілетін қателік және бұл өлшеу құралдарын қолдану дәлдігіне тәуелді емес.

Субьективтік қателік – байқаушының жеке ерекшеліктерімен шартталған қателіктер.

Байқалу сипаты бойынша қателіктер тұрақты және айнымалы болып бөлінеді.

Тұрақты жүйелік қателіктер өзінің мәнін қайта өлшеулерде өзгертпейді. Мысалы, өлшеу құралының дұрыс емес дәлдеуі, есептеудің басталуының дұрыс қойылмауы және т.б.

Айнымалы жүйелік қателіктер қайталап өлшеулерде әртүрлі мәндерді белгілі заңдылықтармен қабылдау. Егер қателіктер қайта өлшеулерде көбейсе, не болмаса азайса, онда бұл прогрестік жүйелік қателік. Периодтық жүйелік қателік периодтық немесе күрделі заң бойынша өзгере алады. Периодтық жүйелік қателіктің пайда болу себебі - сыртқы факторлардың әрекеті және өлшеу құралының құрылымының ерекшеліктері.

Өлшеу нәтижесі әрқашан жүйелік (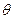) және кездейсоқ () қателіктерден тұрады

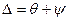. (3.1)

Сондықтан өлшеу нәтижесінің () қателігі жалпы жағдайда кездейсоқ шама ретінде қарастырылуы керек, сонда жүйелік қателік осы шаманың МО болады, ал кездейсоқ қателік – орталықтанған кездейсоқ шама.

3.1 Кездейсоқ шаманың таралу заңдары

Кездейсоқ шаманың толық жазбасы оның таралу заңы болып табылады, демек кездейсоқ қателік y және қателіктер D.

Таралудың әртүрлі заңдары бар. Өлшеу тәжірибесінде қателіктерді таралудің кеңінен таралған заңы қалыпты заң (Гаустың) болып табылады.

Таралудың қалыпты заңының тығыздығының формуласы

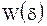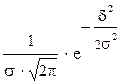= , (3.2)

мұнда s - орташа квадраттық ауытқу;

d - кездейсоқ қателік.

Кездейсоқ шаманы таралудың қалыпты заңының сызбасы 3.1. суретінде көрсетілген.

    W (d)

s = 0.01

s = 0.02

		δ

3.1 сурет – Таралудың қалыпты заңының сызбасы

s қаншалықты аз болса, өлшеулер соншалықты дәлірек орындалады (көбіне шағын кездейсоқ қателіктер кездеседі).

Кездейсоқ шаманы таралудың теңестірілген заңы салыстырмалы түрде жиі кездеседі, оның сызбасы 3.2 суретте берілген.

W(d)

d

0

3.2 сурет – Таралудың теңестірілген заңының сызбасы

Таралудің теңестірілген заңының ықтималды тығыздығының формуласы

. (3.3)

Өлшенетін шаманың мәндері кейбір шекаралық шектерде әртүрлі, бірақ тең ықтималды болуы мүмкін.

Таралудың басқа заңдары МЕСТ 8.011 – 72 “өлшеулер дәлдігінің” көрсеткіштері және өлшеулер нәтижесін ұсыну формалары.

3.1.1 Таралу заңдарының негізгі сипаттамалары.

Бірқатар бақылаулардың математикалық тосу (МТ) – жекелеген бақылаулардың нәтижелерінің соған қатысты салыстырмалы шашырайтын шамасы.

Егер жүйелік қателіктер болмаса және жекелеген өлшемдердің нәтижелерінің шашырауы тек қана кездейсоқ қателіктермен шартталса, онда мұндай бақылау қатарының математикалық тосу өлшенетін шаманың нақты мәні болады.

Егер 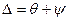, онда мұндай бақылау қатарының математикалық тосу өлшенетін шаманың нақты мәнінен жүйелік қателік мәніне ойысатын болады.

Бірқатар бақылаудың дисперсиясы математикалық тосу айналасындағы жекелеген бақылаулардың нәтижелерінің шашырау дәрежесін көрсетеді. Дисперсия қаншалықты аз болса, соншалықты жекелеген нәтижелер шашырауы аз, соншалықты өлшеулер дәл орындалған болады. Сөйтіп, дисперсия жүргізілген өлшеулердің дәлдігі сипатында қызмет етеді.

Байқаулар қатарының орташа квадраттық ауытқуы 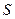. Дисперсияны өлшеу бірлігі өлшенетін шаманың квадраты болып табылатындықтан, дәлдігін бағалау үшін орташа квадраттық ауытқу деп аталатын және дисперсиядан квадраттық түбіріне тең шама пайдаланылады.

3.1.2 Бірқатар бақылаудың негізгі сипаттамаларының бағалары.

Ықтималдық теориясы бойынша математикалық тосуынің бағасы жекелеген бақылаулар нәтижелерінің арифметикалық ортасы - 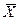болып табылатыны белгілі

, (3.4)

мұнда 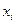- i-й бақылау нәтижесі;

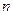- бақылау нәтижелерінің саны.

бақылау қатарының шашырау бағасы келесі формула бойынша есептеледі

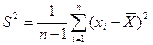. (3.5)

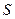бақылау қатарының орташа квадраттық аутқуы бақылау нәтижелерінің кездейсоқ қателіктерінің мөлшерінің негізгі сипаттамасы болып табылады.

Орташа квадраттық ауытқу бағасын s есептеу формуласы

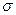= + , (3.6)

n à болғанда (нақтысында n > 30), S² à Д, S à s.

Тақырып бойынша қосымша ақпаратты [1-7,10] алуға болады.

4 дәріс. Өлшеулер қателігі (жалғасы)

Дәрістің мазмұны: дәл және техникалық өлшеулерде қателіктерді бағалау мен есептеу, таралу және кездейсоқ аксиомалары; байқаулар қатарының негізінде өлшеулер нәтижесінің қателіктерін ықтималдылық бағалау, өлшеу құралдардың және өлшеулердің дәлдігін арттыру әдістері.

Дәрістің мақсаты: байқаулар қатарының негізінде өлшеулер нәтижесінің қателіктерін ықтималдылық бағалауын игеру: сенімділік шекаралары, сенімділік интервалы және сенімділік ықтималдылығы; өлшеулердің кездейсоқ және жүйелік қателіктерін азайту әдістері, ӨҚ дәлдігін арттыру әдістері.

4.1 Дәл өлшеулер қателіктерін бағалау және есептеу

Дәл өлшеулер жүйелік қателіктер бола алмайтындай жүргізілуі қажет. Кездейсоқ қателіктер теориясы, тәжірибе деректеріне негізделген, екі аксиомаға тіректенеді.

Кездейсоқ аксиомасы: өлшеулердің саны өте үлкен болса, онда біркелкі жиі кездесетін кездейсоқ қателіктердің шамасы тең, бірақ таңбасы әртүрлі болады: теріс қателіктер саны оң қателіктер санына тең болады.

Таралу аксиомасы: шағын қателіктер үлкенге қарағанда жиірек болады, өте үлкен қателіктер кездеспейді.

Кездейсоқ шаманың, сондай-ақ кездейсоқ қателігінің толық жазбасы таралу заңы болып табылады. Кездейсоқ шаманың таралудың әртүрлі заңдары бар. Өлшеу тәжірибесінде кездейсоқ қателіктерді таралудің ең көбірек таралған заңдары қалыпты және бірқалыпты заңдары болып табылады.

4.1.1 Бірқатар байқаулар негізіндегі өлшеулер нәтижесі қателігінің ықтималдылық бағалары.

Бақылау нәтижелерін өңдеудің мақсаты - өлшенетін шаманың шындық мәнінің орнына қабылдануы мүмкін болатын шаманы және нақты мәнінің шындыққа жақын дәрежесін анықтау.

Нақты мәнінде қайтсе де кездейсоқ қателігі болады. Сондықтан нақты мәннің шындық мәнге жуық дәрежесін ықтималдылық теориясы тұрғысынан қарастыруға болады. Мұндай бағалау болатындай сенімділік интервалын алады. Кездейсоқ қателіктің сенімділік интервалы – берілген сенімділік ықтималмен кездейсоқ қателігінің мәндері түсетін интервал. Егер кездейсоқ қателігінің таралу заңы және осы заңның сипаттамалары белгілі болса, сенімділік интервалын айқындауға болады (3 дәріс).

8.011 – 72 МЕСТ-ке сәйкес сенімділік интервалы өлшеулер дәлдігін білдіретін негізгі формалардың бірі. МЕСТ өлшеу нәтижесін ұсынудың келесі формасын тағайындайды

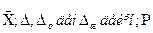, (4.1)

мұнда 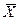– өлшеу нәтижесі (орташа арифметикалық мәні);

D, Dт, Dж – өлшеудің абсолют қателігі мен төменгі және жоғарғы шекаралары;

Р – қателік осы шекараларда болатын сенімділік ықтималдығы.

Ықтималдылық теориясында дәлелдеткен - кездейсоқ қателіктің таралу заңы қалыпты болса, онда шама 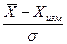, бұл МТ = 0 және Д = 1 қалыпты заңы бойынша таралған 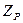кездейсоқ шамасы; ал бұл Стьюдент заңы бойынша таралған 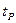кездейсоқ шамасы. 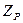және 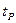үшін кесте бар, ол бойынша сәйкесті 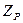және 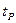үшін Dт, Dж сенімділік интервалының шекарасын Р сенімділік ықтималдығымен анықтайтын мәндерін табуға болады.

, S à s -де, яғни 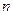бақылау санының артуы мен Стьюдент таралу заңы қалыптыға жуықтайды (тәжірибелік түрде n > 30 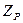- -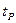ға теңеседі).

Өлшеу тәжірибесінде сенімділік ықтималдықтың әртүрлі мәндерін қолданады: Р = 0,90; 0,95; 0,98; 0,99; 0,9973 және 0,999.

Қалыпты заңда кездейсоқ қателікті таралуда көбіне сенімділік ықтималдылығы 0,9973 болатын +3s дан -3 s -дейінгі сенімділік интервалын пайдаланады. Бұл сенімділік ықтималдығы 370 кездейсоқ қателіктен орташа алғанда тек біреуі ғана = 3 s мәнінен асатын болады. Тәжірибеде жекелеген өлшеулердің саны бірнеше ондағаннан үлкен болуы сирек кездеседі, мұнда «3 сигма заңын» қолданады: қалыпты заң бойынша таралған барлық мүмкін болатын өлшеулердің кездейсоқ қателіктері практикалық тұрғыда 3 s абсолют мәнінен артпайды.

Орындалған өлшеулердің талдауының ең соңғы мақсаты қателіктер мен ықтималдықтың салыстырмалы жиілігінің өлшеуінің соңғылық нәтижесі үшін қабылданатын олардың орта арифметикалық мәнінің қателіктері 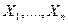өлшенетін шаманың бірқатар мәндерінің бақылау нәтижесінің қателігін анықтаудан тұрады.

4.1.1.1 Бақылау нәтижесінің қателігін (дәлдігін) бағалау.

Бақылау нәтижесінің дәлдігінің бағалауын - 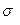бақылаудың нәтижесінің орта квадраттық ауытқуы көрсетеді (3 дәріс). Бақылау нәтижесінің кездейсоқ ауытқуының бағасының дәлдігі және сенімділігі туралы толық түсінік алу үшін сенімділік шекаралары, сенімділік интервалы және сенімділік ықтималдығы көрсетілуі қажет. 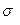белгілі болса, сенімділік шекаралары мына түрде көрсетіледі: төменгі шекарасы (- 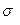), жоғарғы шекарасы (+ 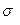) (қысқаша ), бұл шектерден тыс Р=0,683 (немесе 68,3%) ықтималдықпен кездейсоқ ауытқулар мәндері (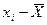) аспайды. Сенімділік интервалы түрінде өрнектеледі. Өлшеу мақсатына байланысты басқа да сенім шекаралары 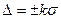берілуі мүмкін, ал бақылау нәтижесінің қателігінің сенімділік интервалы

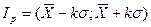, (4.2)

мұнда, 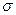- бақылау нәтижесінің орта квадраттық ауытқуы (3.6);

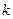- квантиль көбейткіш, мұның мәні кездейсоқ қателіктің таралу заңына байланысты болады.

Сөйтіп, таралудің бірқалыпты заңы үшін 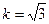және ол сенімділік ықтималдығына тәуелді емес. Таралудің қалыпты заңы үшін 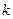сенімділік ықтималдығы (Р) мәніне және бақылау мәндерінің (n) санына тәуелді: n > 30 – 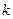= 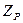; n < 30 - 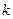= 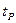(Стьюдент заңы). Ең көп қолданылатын сенімділік ықтималдықтары Р және әртүрлі n үшін 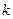мәндері [8,П1-4-1 кесте] келтірілген.

4.1.1.2 Өлшеу нәтижесінің қателігін (дәлдігін) бағалау.

Өлшеу нәтижесі арифметикалық орташа мәніне 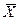тең деп алынады. Қателіктер теориясына сәйкес, өлшеу нәтижесінің орташа квадраттық ауытқу бағасы 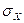бақылаулардың нәтижесінің орташа квадраттық ауытқу бағасынан 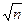есе аз

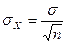. (4.3)

Өлшеу нәтижесінің қателігінің сенімділік интервалы

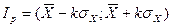, (4.4)

мұнда, 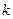- квантиль көбейткіш;

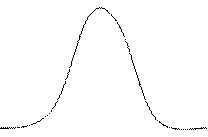
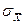- өлшеу нәтижесінің орташа квадраттық ауытқуы.

4.2 Техникалық өлшеулердің қателіктерін есептеу және бағалау

Техникалық өлшеулер - өлшеудің жұмыс құралдарының көмегі арқылы бір рет орындалатын тұрақты шамаларды өлшеу (2 дәріс). Көп жағдайда кездейсоқ қателіктер өлшеудің дәлдігінің айқындаушылары болып табылмайды, сондықтан қат-қабат өлшеулер керегі жоқ. Бір рет өлшеу нәтижесі ретінде өлшеу құралының көрсеткіші алынады. Тура әрекетті көрсететін өлшеу аспабын қолдануда бір реттік өлшеудің нәтижелік қателігі жуықтаған шектік қателікті бағалаумен келесі формула бойынша анықталады

Дата добавления: 2014-12-07