Введение состояния

К счастью, есть выход. Для его нахождения следует обратиться, как и положено, к абстрактному типу данных.

До сих пор список рассматривался как пассивное хранилище информации. Для обеспечения клиентов лучшим сервисом, список должен стать активным, "запоминая" точку выполнения последней операции.

Как отмечалось в этой лекции, без колебаний можно рассматривать объекты как машины с внутренним состоянием и вводить как команды, изменяющие состояние, так и запросы на этом состоянии. В первом решении список уже имел состояние, определяемое его содержимым и модифицируемое командами, такими как put and remove; но, добавив еще несколько компонентов, мы получим лучший интерфейс, делающий класс более простым и эффективным.

Помимо содержимого списка состояние теперь будет включать текущую активную позицию или курсор, интерфейс теперь будет позволять явным образом передвигать курсор.

Рис. 5.7. Список с курсором

Мы полагаем, что курсор может указывать на элемент списка, если таковые имеются, или быть в позиции слева от первого - в этом случае булев запрос before будет возвращать true, или справа от последнего - тогда after принимает значениеtrue.

Примером команды, передвигающей курсор, является процедура search, заменяющая функцию occurrence. Вызовl.search(v) передвинет курсор к первому элементу со значением v справа от текущей позиции курсора, или передвинет его в позицию after, если таких элементов нет. Заметьте, помимо прочего, это решает проблему множественных вхождений, - просто повторяйте поиск столько раз подряд, сколь это необходимо. Для симметрии можно также иметь search_back.

Основные команды манипулирования курсором:

· start и finish, передвигающие курсор в первую и последнюю позицию, если они определены;

· forth и back, передвигающие курсор в следующую и предыдущую позицию;

· go(i), передвигающие курсор в позицию i.

Кроме before и after запросы о позиции курсора включают index, целочисленный номер позиции, начинающийся с 1 для первой позиции, а также булевы запросы is_first и is_last.

Процедуры построения и модификации списка - вставка, удаление, замена - становятся проще, поскольку они не должны заботиться о позиции, а будут действовать на элемент, заданный курсором. Все циклы исчезают! Например, remove не будет теперь вызываться как l.remove (i), а просто l.remove. Необходимо установить точные и согласованные условия того, что случится с курсором при выполнении каждой операции:

· Remove, без аргументов, удаляет элемент в позиции курсора и перемещает курсор к правому соседу, так что значениеindex не изменится в результате.

· Put_right (v: G) вставляет элемент со значением v справа от курсора, не передвигая его, так что значение index не изменится.

· Put_left (v: G) вставляет элемент со значением v слева от курсора, не передвигая его, увеличивая значение indexна единицу.

· Replace (v: G) изменяет значение элемента в позиции курсора. Значение этого элемента может быть получено функциейitem, не имеющей аргументов, которая может быть реализована атрибутом.

Поддержка согласованности: инвариант реализации

При построении класса для фундаментальной структуры данных следует тщательно позаботиться обо всех деталях. Утверждения здесь обязательны. Без них велика вероятность пропуска важных деталей. Например:

· Является ли вызов start допустимым, если список пуст; если да, то каков эффект вызова?

· Что случится с курсором после remove, если курсор был в последней позиции? Неформально мы к этому подготовились, позволяя курсору передвигаться на одну позицию левее и правее списка. Но нам нужны более точные утверждения, недвусмысленно описывающие все случаи.

Ответы на вопросы первого вида будут даны в виде предусловий и постусловий.

Для таких свойств, как допустимые позиции курсора, следует использовать предложения, устанавливающие инвариант реализации. Напомним, он отражает согласованность представления, задающего класс - визави АТД. В данном случае он включает свойство:

0 <= index; index <= count + 1

Что можно сказать о пустом списке? Необходима симметрия по отношению к левому и правому. Одно решение, принятое в ранних версиях библиотеки, состояло в том, что пустой список это тот единственный случай, когда before и after оба истинны. Это работает, но приводит в алгоритмах к частой проверке тестов в форме: if after and not empty. Это привело нас к концептуальному изменению точки зрения и введению в список двух специальных элементов - стражей (sentinel), изображаемых на рисунке в виде специальных картинок.

Рис. 5.8. Список со стражами

Стражи помогают нам разобраться в структуре, но нет причин хранить их в представлении. Реализация рассматривает возможность хранения только левого стража, но не правого, можно также использовать реализацию совсем без стражей, хотя и продолжающую соответствовать концептуальной модели, представленной на предыдущем рисунке.

Часто хочется установить, что некоторый индекс соответствует позиции какого-либо элемента списка. Для этого можно предложить соответствующий запрос:

on_item (i: INTEGER): BOOLEAN is -- Есть ли элемент в позиции i? do Result:= ((i >= 1) and (i <= count)) ensure within_bounds: Result = ((i >= 1) and (i <= count)) no_elements_if_empty: Result implies (not empty) end

Для установления того, что есть элемент списка в позиции курсора, можно определить запрос readable, чье значение определялось бы как on_item (index). Это хороший пример Принципа Списка Требований, поскольку readable концептуально избыточен, то минималистская позиция отвергала бы его, в то же время его включение обеспечивало бы клиентов лучшей абстракцией, освобождая их от необходимости запоминания того, что точно означает индекс на уровне реализации.

Инвариант устанавливает истинность утверждения: not (after and before). В граничном случае пустого списка картина выглядит так:

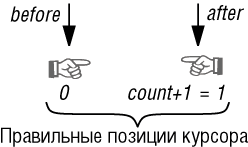
Рис. 5.9. Пустой список со стражами

Итак, пустой список имеет два возможных состояния: empty and before и empty and after, соответствующие двум позициям курсора на рисунке. Это кажется странным, но не имеет неприятных последствий и на практике предпочтительнее прежнего соглашения empty = (before and after), сохраняя справедливость empty implies (before or after).

Отметим два общих урока: важность, как во многих математических и физических задачах, проверки граничных случаев, важность утверждений, выражающих точные свойства проекта. Вот некоторые принципиальные предложения, включенные в инвариант:

0 <= index; index <= count + 1before = (index = 0); after = (index = count + 1)is_first = ((not empty) and (index = 1)); is_last = ((not empty) and (index = count))empty = (count = 0) -- Три следующих предложения являются теоремами, -- выводимыми из предыдущих утверждений:empty implies (before or after)not (before and after)empty implies ((not is_first) and (not is_last))

Этот пример иллюстрирует общее наблюдение, что написание инварианта - лучший способ придти к настоящему пониманию особенностей класса. Утверждения инварианта применимы ко всем реализациям последовательных списков, они будут дополнены еще несколькими, отражающими специфику выбора связного представления.

Последние три предложения инварианта выводимы из предыдущих (см. У5.6). Для инвариантов минимализм не требуется, часто полезно включать дополнительные предложения, если они устанавливают важные, нетривиальные свойства. Как мы видели (см.лекцию 6 курса "Основы объектно-ориентированного программирования"), АТД и, как следствие, реализация класса является теорией, в данном случае теорией связных списков. Утверждения инварианта выражают аксиомы теории, но любая полезная теория имеет также и интересные теоремы.

Конечно, если вы хотите проверять инварианты в период выполнения, то рассматривать дополнительные предложения имеет смысл, если вы не доверяете обоснованности теории. Но это делается только на этапах разработки и отладки. В производственной системе нет причин наблюдения за инвариантами.

Дата добавления: 2014-12-07