
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
МЕХАНИЗМОВ 2 страница
|
|
|
|
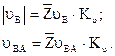
Направление скорости 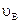 определяется при параллельном переносе вектора
определяется при параллельном переносе вектора 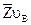 в точку В механизма (рис. 2.2, а). Т.к. вектор
в точку В механизма (рис. 2.2, а). Т.к. вектор 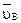 в точке В механизма направлен в сторону положительной полуоси
в точке В механизма направлен в сторону положительной полуоси  , знак скорости
, знак скорости 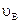 будет положительным.
будет положительным.
Модуль угловой скорости звена 2 будет
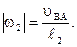 (2.29)
(2.29)
Направление 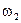 находится по вектору
находится по вектору  . На рис. 2.2, а
. На рис. 2.2, а 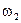 направлена по часовой стрелке.
направлена по часовой стрелке.
Скорость точки 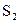 определяется с помощью векторного уравнения:
определяется с помощью векторного уравнения:
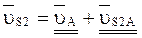 (2.30)
(2.30)

Здесь скорость относительного движения точки 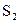
 находится методом пропорционального деления отрезка ав на плане скоростей, изображающего относительную скорость
находится методом пропорционального деления отрезка ав на плане скоростей, изображающего относительную скорость 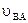
 (2.31)
(2.31)
Действительная скорость  определяется как
определяется как
 (2.32)
(2.32)
Для рассматриваемого примера численное значение скорости 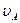 равно
равно
 =12,56*0,175=2,198 м/с
=12,56*0,175=2,198 м/с 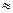 2,2 м/с.
2,2 м/с.
Если на плане скоростей (рис.2.2,б) известную скорость 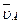 изобразить отрезком длиной 66 мм, то получим:
изобразить отрезком длиной 66 мм, то получим:

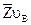 =51 мм;
=51 мм; 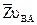 =47 мм;
=47 мм;
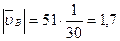 м/с.
м/с.
Так как вектор 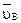 в точке В механизма направлен в сторону положительной полуоси
в точке В механизма направлен в сторону положительной полуоси  ,знак будет положительным:
,знак будет положительным:
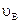 =1,7 м/с
=1,7 м/с
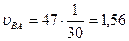 м/с;
м/с; 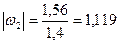
 .
.
Угловая скорость 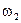 направлена по часовой стрелке, поэтому имеет знак «минус»:
направлена по часовой стрелке, поэтому имеет знак «минус»:
 1/с;
1/с;
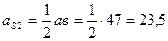 мм;
мм; 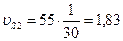 м/с.
м/с.
Сравнение с результатами аналитического метода расчета дает ошибку не более 3%.
2.2.3. Определение ускорений
Построение плана ускорений позволяет определить линейные ускорения точек 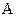 ,
,  и
и 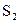 , а также угловое ускорение звена 2.
, а также угловое ускорение звена 2.
Ускорение точки 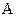 кривошипа складывается из суммы нормальной
кривошипа складывается из суммы нормальной  и тангенциальной
и тангенциальной 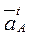 составляющих
составляющих
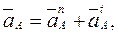 (2.33)
(2.33)
где 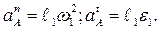
Нормальные составляющие ускорений всегда направлены по радиусу к центру вращения, а тангенциальные составляющие перпендикулярны радиусу и направлены в сторону углового ускорения.
Ускорение точки В, принадлежащей звену 2, можно представить в виде векторной суммы ускорений переносного  и относительного
и относительного 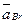 движений
движений
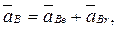 (2.34)
(2.34)
где 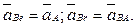
Относительное ускорение точки  также состоит из двух составляющих
также состоит из двух составляющих
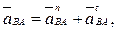 (2.35)
(2.35)
где 
С учетом приведенных выше формул и в случае 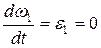 окончательно получим
окончательно получим 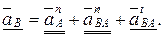 (2.36)
(2.36)

Как и раньше, одной чертой подчеркнуты векторы, известные только по направлению, а полностью известные векторы подчеркнуты двумя чертами.
Построение плана ускорений начинаем с выбора масштабного коэффициента плана ускорений 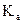 по любой известной величине – либо по
по любой известной величине – либо по  , либо по
, либо по  . Пусть
. Пусть
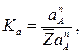 (2.37)
(2.37)
где 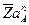 - длина отрезка, изображающего ускорение
- длина отрезка, изображающего ускорение  .
.
Тогда величина отрезка 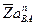 , изображающего известное ускорение
, изображающего известное ускорение  , будет
, будет
 (2.38)
(2.38)
Из произвольной точки полюса плана ускорений  (рис. 2.2, в) откладываем отрезок
(рис. 2.2, в) откладываем отрезок 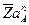 в направлении к центру вращения звена 1 – точке
в направлении к центру вращения звена 1 – точке 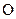 . Так как
. Так как 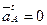 и, следовательно,
и, следовательно, 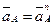 , отрезок
, отрезок 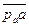 изображает полное ускорение точки
изображает полное ускорение точки 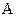 .
.
Из конца отрезка 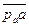 параллельно
параллельно  по направлению к центру относительного вращения звена 2 – точке
по направлению к центру относительного вращения звена 2 – точке 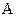 откладываем отрезок
откладываем отрезок 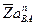 и из его конца перпендикулярно
и из его конца перпендикулярно  проводим линию действия тангенциальной составляющей относительного ускорения
проводим линию действия тангенциальной составляющей относительного ускорения  . Затем из полюса плана
. Затем из полюса плана  параллельно
параллельно  проводим линию действия абсолютного ускорения точки
проводим линию действия абсолютного ускорения точки  . Точка b, полученная на пересечении этих линий, определяет концы отрезков
. Точка b, полученная на пересечении этих линий, определяет концы отрезков 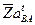 и
и 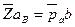 , изображающих соответствующие ускорения. Величины этих ускорений будут
, изображающих соответствующие ускорения. Величины этих ускорений будут
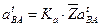 и
и 
Так как вектор ускорения 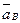 направлен в сторону отрицательной полуоси
направлен в сторону отрицательной полуоси  , то знак ускорения
, то знак ускорения 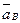 будет отрицательным.
будет отрицательным.
Соединив прямой точки 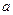 и b плана ускорений, получим отрезок
и b плана ускорений, получим отрезок  , изображающий полное относительное ускорение
, изображающий полное относительное ускорение  . Его величина будет
. Его величина будет

Величина углового ускорения звена 2 определяется из уравнения
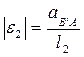 . (2.39)
. (2.39)
Перенеся вектор ускорения  в точку
в точку  механизма и рассматривая движение точки В относительно точки
механизма и рассматривая движение точки В относительно точки 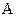 , можно определить направление ускорения
, можно определить направление ускорения 
Ускорение точки 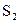 определяется из векторного уравнения
определяется из векторного уравнения
 (2.40)
(2.40)

Величина относительного ускорения 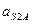 находится аналогично скорости
находится аналогично скорости  - методом пропорционального деления отрезка
- методом пропорционального деления отрезка 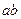 , изображающего относительное ускорение
, изображающего относительное ускорение 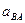
 (2.41)
(2.41)
или на рис. 2.2, в

Полное ускорение точки S2 определяется как
 (2.42)
(2.42)
Для рассматриваемого примера расчеты дают следующие значения параметров:
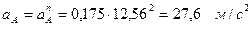 ;
;
 .
.
Возьмем отрезок  а
а  =82,8 мм, тогда масштабный коэффициент будет равен
=82,8 мм, тогда масштабный коэффициент будет равен 
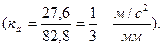
Отрезок, изображающий известное ускорение  :
:
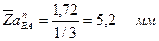 .
.
Искомые ускорения будут:
 ;
;
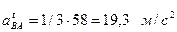 ;
;
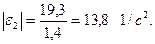
Так как вектор ускорения  направлен в сторону отрицательной полуоси
направлен в сторону отрицательной полуоси  , то
, то
 .
.
Угловое ускорение  направлено по часовой стрелке, поэтому
направлено по часовой стрелке, поэтому
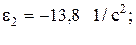
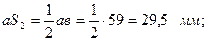

Сравнение результатов расчета со значениями, полученными аналитическим методом, дает максимальную ошибку не более 3%.
3. СИЛОВОЙ АНАЛИЗ МЕХАНИЗМА
Задачей силового анализа рычажных механизмов является определение сил, действующих в кинематических парах механизма, уравновешивающей силы или уравновешивающего момента, которые надо приложить к ведущему звену для обеспечения требуемого закона движения ведомого звена.
Силовой расчет механизма в дальнейшем позволит решить следующие инженерные задачи: 1) расчет звеньев механизма на прочность, жесткость, износоустойчивость и т.п.; 2) расчет подвижных соединений звеньев на долговечность; 3) выбор мощности двигателя и т.д.
При проектировании механизма силовой анализ выполняется в два этапа. На первом этапе определяют силы в кинематических парах без учета сил трения, зависящих от усилий в кинематических парах, учитывая лишь постоянные составляющие, заданные в технических условиях.
Используя результаты первого этапа, определяют силы и моменты трения, зависящие от сил реакций, и на втором этапе с их учетом определяют истинные реакции в кинематических парах.
При использовании кинетостатического метода в уравнения равновесия, называемые уравнениями кинетостатики, входят не только внешние силы и моменты, силы в кинематических парах, но и силы и моменты сил инерции.
Для кинетостатической определимости плоский механизм не должен иметь избыточных связей.
Силовой расчет механизма проводят в соответствии с его структурным составом, т.е. расчет начинают со структурной группы, наиболее удаленной от начального звена, и заканчивают расчетом первичного механизма.
3.1 Силовой анализ без учета сил трения, зависящих от сил, действующих в кинематических парах.
Для первого этапа силового анализа проведем расчет несколькими методами:
1) для расчетного положения механизма графоаналитическим методом определим силы во всех кинематических парах и уравновешивающий момент, который необходимо приложить к начальному зевну;
2) основываясь на методе возможных перемещений, определим аналитическим и графоаналитическим способами уравновешивающий момент для того же расчетного положения механизма.
3.1.1. Графоаналитический метод силового анализа механизма
Для расчетного положения механизма необходимо определить все силы и моменты сил, действующие на звенья механизма.
1. Силы тяжести
 (
(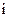 =2,3). (3.1)
=2,3). (3.1)
2. Силы от действия горизонтальной и вертикальной перегрузок:
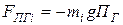 ,
,  . (3.2)
. (3.2)
3. Главные векторы и главные моменты инерционных сил, к которым приводятся силы инерции, действующие на каждое звено механизма. Для звеньев 2 и 3

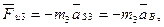 (3.3)
(3.3)
где 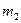 и
и 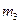 -массы звеньев 2 и 3;
-массы звеньев 2 и 3;  и
и 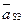 -ускорения центров масс звеньев (для звена 3 точка
-ускорения центров масс звеньев (для звена 3 точка 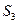 совпадают с точкой В);
совпадают с точкой В);  -угловое ускорение звена 2;
-угловое ускорение звена 2;  -момент инерции масс звена 2 относительно оси, проходящей через центр масс и перпендикулярной плоскости движения звена, который определяется по формуле
-момент инерции масс звена 2 относительно оси, проходящей через центр масс и перпендикулярной плоскости движения звена, который определяется по формуле
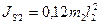 . (3.4)
. (3.4)
4. Сила трения на ползуне
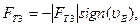 (3.5)
(3.5)
где 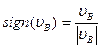 .
.
5. Сила сопротивления на ползуне:
для нерабочего хода ползуна 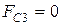 ;
;
для рабочего хода 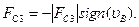 (3.6)
(3.6)
Здесь  -модуль силы сопротивления, соответствующий расчетному положению механизма. Для определения значения этой силы необходимо построить приближенный график параболической зависимости силы сопротивления от координаты точки В
-модуль силы сопротивления, соответствующий расчетному положению механизма. Для определения значения этой силы необходимо построить приближенный график параболической зависимости силы сопротивления от координаты точки В  (
(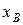 ), используя три значения функции
), используя три значения функции  для трех значений аргумента
для трех значений аргумента 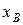 , данные в задании.
, данные в задании.
График зависимости  (
(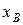 ) представлен на рис.3.1.
) представлен на рис.3.1.
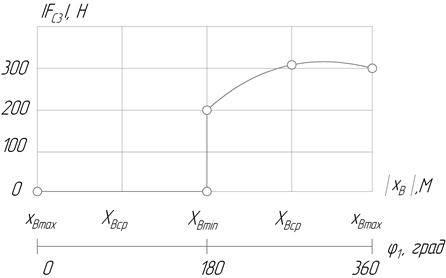
Рис. 3.1. Зависимость силы сопротивления от положения ползуна
Знак «минус» везде учитывает направление силового параметра, противоположное направлению соответствующего кинематического параметра.
Численные значения сил и моментов сил для расчетного положения рассматриваемого механизма (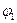 =
= 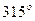 ) будут следующими:
) будут следующими:
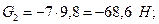

 ;
;  ;
; 
 ;
; 

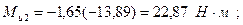
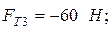
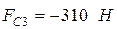 (см.рис.3.1);
(см.рис.3.1); 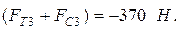
Малыми величинами, которые составляют не более (5…10)% от максимальной известной силы, можно пренебречь.
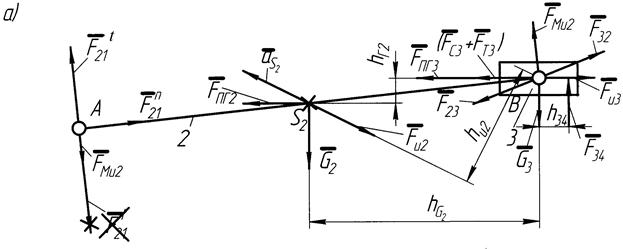
Силовой расчет механизма следует начать с двухповодковой группы, состоящей из звеньев 2 и 3. Схема структурной группы, изображенной в масштабе со всеми приложенными силами, представлена на рис. 3.2,а. Определению подлежат силы реакции  ,
, 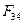 и
и  .
.
Задача нахождения сил и плеча 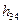 является статически определимой задачей, поскольку для группы из двух звеньев можно составить 6 уравнений равновесия, и определению подлежат 6 неизвестных - величины и направления сил реакций во вращательных кинематических парах А и В, величина и точка приложения силы
является статически определимой задачей, поскольку для группы из двух звеньев можно составить 6 уравнений равновесия, и определению подлежат 6 неизвестных - величины и направления сил реакций во вращательных кинематических парах А и В, величина и точка приложения силы 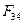 в поступательной кинематической паре ползун – неподвижные направляющие ползуна.
в поступательной кинематической паре ползун – неподвижные направляющие ползуна.
Для удобства проведения расчета главный момент сил инерции можно заменить парой сил, приложенных в точках А и В звена 2. Значения сил будут
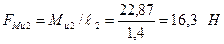 .
.
При графоаналитическом методе расчета следует неизвестную силу реакции  предоставить в виде двух составляющих: нормальной
предоставить в виде двух составляющих: нормальной 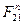 , направленной вдоль звена, и касательной
, направленной вдоль звена, и касательной 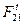 , направленной перпендикулярно звену.
, направленной перпендикулярно звену.
Все неизвестные силы реакции на рис. 3.2, а направлены произвольно. Если из расчета какая-либо сила получится со знаком «минус», это значит, что ее действительное направление противоположно принятому.
Для системы сил, действующих на звено 2, составим уравнение моментов относительно точки 
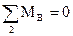 . (3.7)
. (3.7)
Если условиться, что моменты, направленные против часовой стрелки, считаются положительными, а по часовой стрелке - отрицательными, то уравнение моментов будет иметь вид
 ,
,
где неизвестная составляющая силы  направлена произвольно – вниз от точки
направлена произвольно – вниз от точки 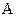 .
.
В развернутом виде уравнение перепишется как
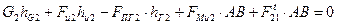 .
.
Откуда неизвестная сила  будет
будет
 . (3.8)
. (3.8)
 точкой В);центров масс звеньев (для звена 3 точка ься сисилы во всех кинематических парах
точкой В);центров масс звеньев (для звена 3 точка ься сисилы во всех кинематических парах
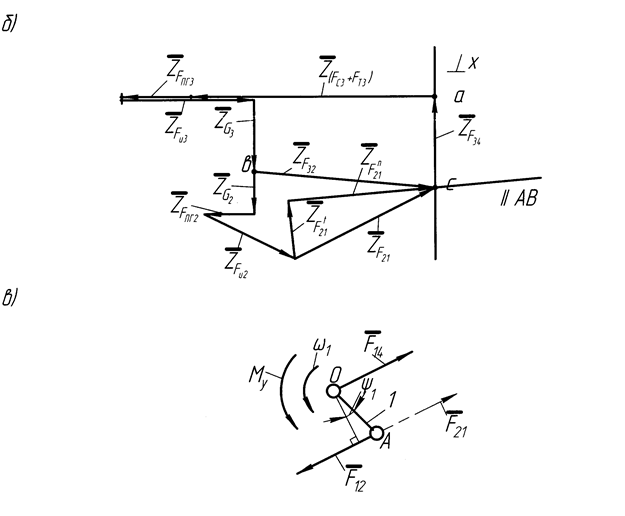
Рис.3.2. Схема к кинетостатическому расчету двухповодковой группы,
ведущего звена и план сил
Здесь через 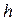 с индексами обозначены плечи соответствующих сил относительно точки
с индексами обозначены плечи соответствующих сил относительно точки  . Как видно из формулы для
. Как видно из формулы для  , плечи сил могут быть взяты непосредственно из рисунка группы (рис.3.2, а), невзирая на масштаб его построения.
, плечи сил могут быть взяты непосредственно из рисунка группы (рис.3.2, а), невзирая на масштаб его построения.
Следует отметить, что при определении численных значений сил реакций, как  , так и других, все силы следует брать по модулю, так как знак силы указывает на ее действительное направление, а на схеме механизма знак силы был учтен при изображении ее на рисунке.
, так и других, все силы следует брать по модулю, так как знак силы указывает на ее действительное направление, а на схеме механизма знак силы был учтен при изображении ее на рисунке.
Численное значение касательной составляющей  для рассматриваемого примера будет
для рассматриваемого примера будет
 .
.
Знак «минус» означает, что сила  должна быть направлена в противоположную от выбранного направления сторону, т.е. от точки А вверх, что показано на рис. 3.2, а.
должна быть направлена в противоположную от выбранного направления сторону, т.е. от точки А вверх, что показано на рис. 3.2, а.
Для определения величин нормальной составляющей силы в точке 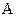
 и силы
и силы  составим векторное уравнение равновесия структурной группы, сгруппировав силы по звеньям:
составим векторное уравнение равновесия структурной группы, сгруппировав силы по звеньям:
 . (3.9)
. (3.9)
Или
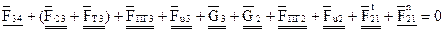 .
.

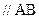
В уравнении силы, известные по величине и направлению, подчеркнуты двумя чертами, а известные лишь по направлению - одной чертой.
Решим векторное уравнение графически - путем построения многоугольника сил (рис.3.2,б). Для этого необходимо выбрать масштабный коэффициент построения плана сил 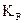 , используя любую известную силу, лучше максимальную: у нас
, используя любую известную силу, лучше максимальную: у нас 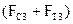 ,
,
 . (3.10)
. (3.10)
Если для рассматриваемого примера отрезок 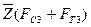 , изображающий сумму сил
, изображающий сумму сил 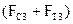 =370 Н, выбрать равным 74 мм, то масштабный коэффициент плана сил будет «удобным» числом:
=370 Н, выбрать равным 74 мм, то масштабный коэффициент плана сил будет «удобным» числом:
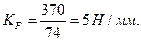
Тогда отрезки, изображающие остальные известные силы, будут
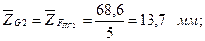


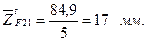
Построение силового многоугольника начнем с линии действия силы 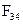 , перпендикулярной оси
, перпендикулярной оси  (рис. 3.2, б). Из произвольной точки а на этой линии, которая является точкой конца отрезка, изображающего вектор силы
(рис. 3.2, б). Из произвольной точки а на этой линии, которая является точкой конца отрезка, изображающего вектор силы  , проведем вектор
, проведем вектор 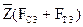 , известный по величине и направлению. Из конца этого вектора проведём следующий известный вектор
, известный по величине и направлению. Из конца этого вектора проведём следующий известный вектор  и так далее, согласно векторному уравнению сил. Из конца последнего известного вектора
и так далее, согласно векторному уравнению сил. Из конца последнего известного вектора 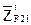 проводим линию действия силы
проводим линию действия силы  , параллельную
, параллельную  . Пересечение в точке с этой линии и первой, перпендикулярной оси
. Пересечение в точке с этой линии и первой, перпендикулярной оси  , определяет искомые отрезки
, определяет искомые отрезки  и
и  . Измерив их длины, определим значения сил:
. Измерив их длины, определим значения сил:
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 511; Нарушение авторских прав?; Мы поможем в написании вашей работы!