Кинетическая энергия тела

Энергия.

Из опыта известно, что тела часто оказываются в состоянии совершать работу над другими телами.

ОПРЕДЕЛЕНИЕ: Физическая величина, характеризующая способность тела или системы тел совершать работу, называется энергией.

Пример: 1) Катящийся шар обладает энергией, т.к., сталкиваясь с другим телом, перемещает его, т.е. совершает работу.

2) Растянутая пружина также обладает энергией, т.к. после устранения деформирующей силы, совершает работу по перемещению своих частей (витков) или какого-либо другого тела.

3) система, состоящая из Земного шара и расположенного на некоторой высоте тела, обладает энергией, т.к. при устранении связи, удерживающей тело на высоте, это тело начнет двигаться и может совершить работу.

Итак, названные тела обладают энергией независимо от того, совершают они в данный момент времени работу или нет. Энергия характеризует способность системы к совершению работы при переходе из одного состояния в другое.

Если в первом состоянии энергия системы Е₁, а во втором Е₂, то

А = Е₂ - Е₁.

Если работа внешних сил A > 0, то энергия системы возрастает Е₂ ‑ Е₁ > 0.

Если A<0 (система совершает работу), то энергия системы убывает. Е₂-Е₁<0, т.е. убыль энергии в этом случае численно равна работе против тех сил, которые препятствуют движению тела. Следовательно, система может совершать работу только за счет изменения своей энергии.

Энергия тела может быть обусловлена двумя причинами:

1. Во-первых, движением тела с некоторой скоростью v. Энергия этого вида называется кинетической энергией (от греческого «кинетикос» – относящийся к движению).

2. Во-вторых, взаимным расположением тел или частей тела и характером их взаимодействия (или более, строго говоря, нахождением тела в потенциальном поле сил). Энергия этого вида называется потенциальной (от латинского «potential» – возможность).

Замечание: Поле сил называется потенциальным, если работа, совершаемая над телом силами, зависящими только от положения тела, не зависит от пути, а определяется только начальным и конечным положением тела в пространстве. А сами силы называются консервативными.

Далее рассмотрим введенные понятия более подробно.

Рассмотрим простейшую систему, состоящую из одной частицы (материальной точки).

Напишем уравнение движения частицы . Здесь 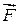– результирующая всех сил, действующих на тело. Умножим это уравнение на перемещение частицы . Тогда . Здесь – есть приращение скорости 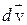за время dt.

Соответственно,

.

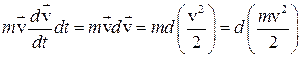После этого получаем:

(3.9)

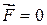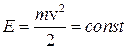Если система замкнута, то , следовательно, , а сама величина . Эта величина называется кинетической энергией частицы.

Говорят, что для изолированной системы кинетическая энергия является интегралом движения (т.е. остается неизменной).

Если на частицу действует сила 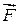, то кинетическая энергия не остается постоянной. Проинтегрируем соотношение (3.9) вдоль некоторой траектории от точки 1 до точки 2.

.

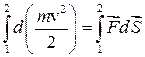Левая часть этого равенства представляет собой разность значений кинетической энергии в точках 2 и 1, т.е. приращение кинетической энергии на пути 1 – 2. Учтя это, получим:

,

где А – работа силы на пути 1®2, поэтому иногда пишут вместо А ® А₁₂.

Итак:

Работа результирующей всех сил, действующих на частицу, идет на приращение кинетической энергии частицы: А₁₂ = Т₂ - Т₁.

Энергия имеет такую же размерность, как и работа.

Дата добавления: 2014-12-07