Метод сеток

Построение двумерных температурных полей.

Рассмотрим два метода, которые могут быть сравнительно просто использованы в инженерной практике для расчета двумерных температурных полей конструкций.

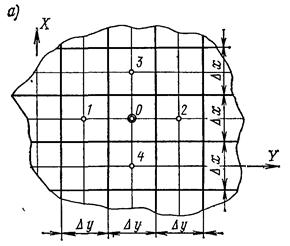
Область двумерного сечения конструкции, для которой требуется пост-

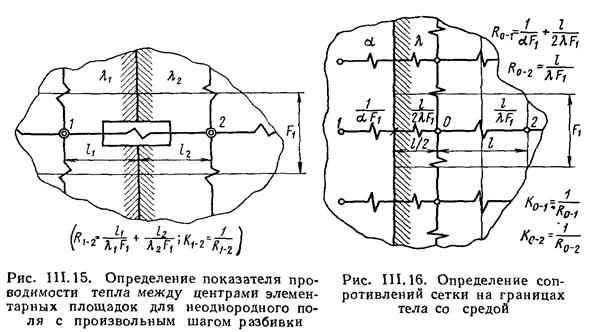
роить температурное поле, делят на элементарные площадки, центры которых соединяют сосредоточенными термическими сопротивлениями (рис. а). Таким образом, переходят от поля к тепловой сетке (рис. б) с сосредоточенными параметрами.

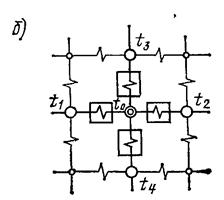
Уравнение стационарной теплопроводности для такой сетки (поле однородное) в конечных разностях имеет вид

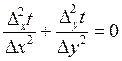
Вторые конечные разности приращения температуры равны:

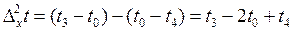
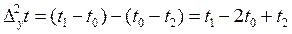
Решение уравнения относительно температуры в произвольном узле сетки, если шаг сетки одинаковый, может быть получено в виде

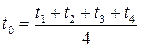
Таким образом, при однородном поле температура в произвольном узле сетки равна среднеарифметическому значению температуры в соседних узлах.

Для конструкции неоднородной и с произвольным шагом разбивки сетки решение конечноразностного уравнения относительно to имеет вид

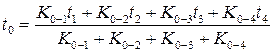
где 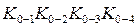- показатели проводимости соединений тепловой сетки

между соответствующими узлами в центрах элементарных площадок.

Из уравнения следует, что в общем случае температура в произвольном узле равна средневзвешенному (по проводимостям связей) значению температур в соседних узлах. Это общее уравнение может быть использовано, в том числе для определения температуры в узлах, граничащих с поверхностью ограждения, а также в узлах на стыках материальных слоев.

Показатель проводимости К между узлами должен определяться по правилу сложения параллельно и последовательно расположенных термических сопротивлений. Может быть два случая определения термических сопротивлений. Сопротивление теплопроводности однородного объемного элемента равно

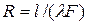
где 1-протяженность элемента в направлении, в котором определяется сопротивление; F - площадь элемента в сечении, перпендикулярном этому направлению.

Сопротивление теплообмену на поверхности элемента, граничащего

с воздухом, равно

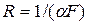
где α- коэффициент теплообмена на этой поверхности; F - площадь поверхности элемента.

Расчет состоит в решении системы линейных уравнений, состоящей из стольких уравнений, сколько узлов в принятой тепловой сетке. Систему уравнений удобнее всего решать методом последовательного приближения, сущность которого в следующем. Сначала задают ориентировочные значения температур в узлах тепловой сетки, затем постепенно уточняют эти значения, добиваясь удовлетворения уравнений системы.

Наиболее удобным является метод релаксации, который состоит в определении дебаланса в каждой точке, с постепенным его уменьшением и доведением до величин, близких к нулю, изменением температуры в данной и соседних точках.

Для простейшего случая однородной конструкции дебаланс в узле Δt можно записать в виде

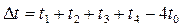
Из этого уравнения видно, что изменением температуры в каждой из соседних точек (1, 2, 3, 4) на единицу можно скорректировать Δt на + -1, а изменением температуры в узловой точке (О) на +- 4. Это обстоятельство является, по существу, ключом к последовательности вычислений. После задания в узлах ориентировочных температур и вычисления Δt изменяют температуры, начиная с узлов наибольшего дебаланса и, перемещаясь от узла к узлу, уменьшают его.

Дата добавления: 2014-12-07