
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры решения задач о взаимном положении прямых
|
|
|
|
Определение по чертежу перпендикулярно скрещивающихся прямых (комплексные задачи)
Определение по чертежу скрещивающихся прямых (позиционные задачи)
Признак скрещивающихся прямых на чертеже (рис. 3.17): точки пересечения одноимённых проекций скрещивающихся прямых не лежат на одной линии связи, а являются слиянием двух проекций конкурирующих точек этих прямых.
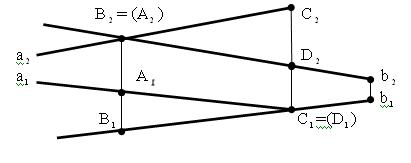
Рис. 3.17
Признак перпендикулярно скрещивающихся прямых (рис. 3.18): если одна из перпендикулярно скрещивающихся прямых параллельна какой-либо плоскости проекций, то на этой плоскости угол между их проекциями остаётся без искажения прямым.

Рис. 3.18
Задача 1 (рис. 3.19). Определить взаимное положение отрезков АВ и CD, если заданы их горизонтальные и фронтальные проекции.


Рис. 3.19
Решение задачи.
Так как заданные отрезки принадлежат профильным прямым, то построим профильные проекции этих отрезков, которые показывают, что заданные прямые линии скрещиваются.
Задача 2 (рис. 3.20). Заданную прямую a пересечь фронталью f, проходящей через точку M.

Рис. 3.20
Решение задачи.
1. M 
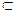 f
f 
 л.с., f
л.с., f 
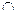 a
a  = N
= N  ;
;
2. N 
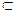 a
a  , f
, f  = N
= N  M
M  .
.
Задача 3 (рис. 3.21). Провести через точку М, у которой задана её фронтальная проекция М  , горизонталь h так, чтобы h
, горизонталь h так, чтобы h 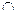 a, h
a, h  a. Определить горизонтальную проекцию М
a. Определить горизонтальную проекцию М  .
.

Рис. 3.21
Решение задачи.
1. М 
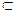 h
h 
 л.с., h
л.с., h 
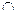 a
a  = N
= N  ;
;
2. N 
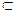 a
a  , MN = h
, MN = h  a
a 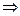 M
M  N
N 
 a
a  .
.
Задача 4 (рис. 3.22). Заданы профильно конкурирующие точки А и В, через которые проходят взаимно перпендикулярные прямые a и b. Построить недостающие проекции этих прямых.

Рис. 3.22
Решение задачи.
1. В 
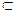 h
h 
 л.с.
л.с.
a  h
h 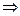 А
А 
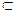 а
а 
 h
h  .
.
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 893; Нарушение авторских прав?; Мы поможем в написании вашей работы!