
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пересечение плоской поверхности с прямой линией на чертеже
|
|
|
|
Параллельные плоскости на чертеже
Параллельные прямая и плоскость на чертеже
Определение по чертежу взаимного положения плоскостей и прямых линий
Определение параллельности геометрических фигур на чертеже связано с решением позиционных задач.
Признак: прямая параллельна заданной плоскости, если она параллельна одной из прямых этой плоскости.
Пример (рис. 5.21). Через точку M провести прямую a || 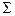 (ABC).
(ABC).
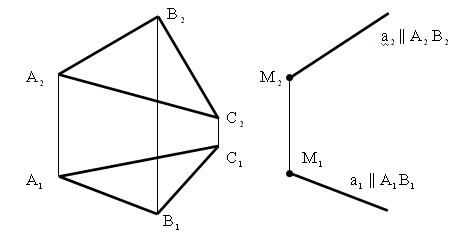
Рис. 5.21
Алгоритм решения:
1. a  || A
|| A  B
B  ;
;
2. a  || A
|| A  B
B 
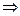 a ||
a || 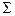 (ABC).
(ABC).
Признак: плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны соответствующим двум пересекающимся прямым другой плоскости.
Пример (рис. 5.22). Через точку М провести плоскость 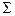 ||
|| 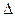 (a || b).
(a || b).

Рис. 5.22
Алгоритм решения:
1. 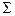
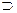 h
h 
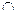 a;
a;
2. M 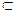 h || h
h || h  ;
;
3. M 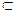 c || a
c || a 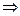 M = h
M = h 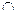 c =
c = 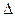 ||
|| 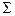 .
.
Определение результатов пересечения геометрических фигур на чертеже связано с решением позиционных задач третьего типа, получивших название «главные позиционные задачи» – ГПЗ. В зависимости от типа пересекающихся фигур различают две группы ГПЗ:
1. Задачи на пересечение плоскостей (плоских поверхностей) с прямыми линиями (1.ГПЗ). Результаты пересечения – точки.
2. Задачи на пересечение плоских поверхностей (2.ГПЗ). Результаты пересечения – прямые линии.
При этом различают ГПЗ с тремя вариантами расположения геометрических фигур относительно основных плоскостей проекций:
ГПЗ.1 - обе пересекающиеся геометрические фигуры занимают проецирующее положение ( ,
,  );
);
ГПЗ.2 - одна из пересекающихся фигур занимает проецирующее, а другая - общее положение ( , не
, не  );
);
ГПЗ.3 - обе пересекающиеся фигуры занимают общее положение (не  , не
, не  ).
).
Для каждого варианта и разновидности ГПЗ разработан свой типовой порядок (алгоритм) решения задач.
В данном разделе рассматриваются задачи на пересечение прямой линии с плоской поверхностью (1.ГПЗ).
Решение задач 1.ГПЗ. 1 ( ,
,  )
)
Алгоритм решения
1.Искомые проекции точек пересечения проецирующих геометрических фигур уже изображены на чертеже по принадлежности их главным проекциям.
2.Определяют (при необходимости) видимость элементов геометрических фигур.
Пример (рис. 5.25). На трёх картинном чертеже определить проекции точки пересечения прямой a с плоскостью 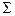 (ABC).
(ABC).

Рис. 5.25
Алгоритм решения:
1. a 
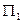
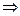 P
P  = a
= a  ;
;
2. 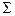

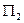
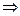 P
P  = a
= a 
 ;
;
3. P 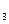
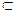 a
a 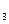 .
.
Решение задач 1.ГПЗ. 2 ( , не
, не  )
)
Алгоритм решения
1.Одна из искомых проекций точки пересечения геометрических фигур уже изображена на чертеже по её принадлежности главной проекции проецирующей фигуры.
2.Вторую проекцию строят по признаку её принадлежности геометрической фигуре общего положения.
3.Определяют видимость элементов заданных фигур.
Пример 1 (рис. 5.26). Определить проекции точки пересечения прямой а с плоскостью 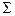 (ABC).
(ABC).

Рис. 5.26
Алгоритм решения:
1. 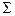

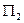
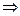 P
P  =
= 
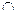 a
a 
2. P 
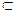 a
a  .
.
Пример 2 (рис. 5.27). Определить проекции точек пересечения
прямой а с пирамидой 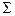 (ABC).
(ABC).
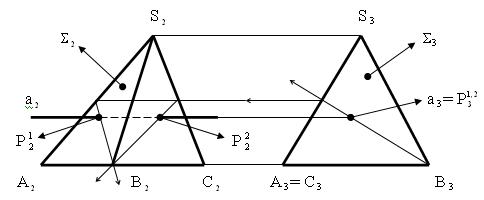
Рис. 5.27
Алгоритм решения:
1. a 
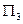
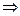 a
a 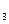 = P
= P 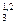 ;
;
2. P 
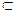 S
S  A
A  B
B  ;
;
3. P 
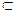 S
S  B
B  C
C  .
.
Решение задач 1.ГПЗ. 3 (не  , не
, не  )
)
Эти главные позиционные задачи решают с использованием метода введения дополнительной (вспомогательной) плоскости – посредника.
Алгоритм решения
Заданную прямую заключают во вспомогательную проецирующую плоскость – посредник.
Строят линию пересечения заданной поверхности с плоскостью – посредником.
Определяют точку (точки) пересечения заданной прямой с полученной линией, которая и является искомым решением задачи.
Определяют видимость элементов заданных геометрических фигур.
Пример (рис. 5.28). Определить точку пересечения прямой а с плоскостью общего положения 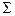 (АВС).
(АВС).

Рис. 8.28
Алгоритм решения:
1. a 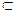
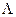

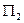 ;
;
2. 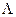
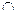
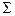 = 12 = m;
= 12 = m;
3. a 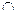 m =P
m =P 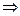 a
a 
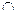 m
m  = P
= P  ; P
; P 
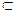 a.
a.
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 579; Нарушение авторских прав?; Мы поможем в написании вашей работы!