Вопрос 1. Понятие «сложные проценты», формула сложных процентов, формула наращения

Тема 4. Сложные проценты

Цель: Изучить формулы наращения и дисконтирования по сложным процентам. Рассмотреть понятие «капитализация», виды дисконтирования.

Ключевые слова: сложные проценты, формула наращения, математическое дисконтирование, банковский учет, непрерывное наращение и дисконтирование, начисление процентов смешанной схеме, начисление процентов по номинальной ставке, дисконт, непрерывное наращение.

Вопросы:

1. Понятие «сложные проценты», формула сложных процентов,

2. База начисления процентов и понятие капитализации

3. Дисконтирование по сложной ставке процента: математическое дисконтирование, банковский учет

4. Непрерывное наращение и дисконтирование

Сложные проценты – применяются в долгосрочных финансово-кредитных операциях, если проценты не выплачиваются периодически сразу после их начисления за прошедший интервал времени, а присоединяются к сумме долга. Присоединение начисленных процентов к сумме, которая служила базой для их начисления, называется капитализацией процента.

Пусть Р – первоначальная сумма долга, через один год сумма долга с процентами составит Р(1+i)ⁿ.

Формула сложных процентов: 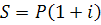ⁿ, где

S – наращенная сумма; 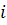– годовая ставка сложных процентов; n – срок займа;

– множитель наращения

На практике чаще всего применяются дискретные проценты за одинаковые интервалы времени.

Если ставка сложных процентов меняется во времени, то применяется формула:

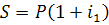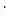
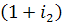^{n1 n2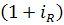} … ^nR, где

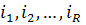– последовательные значения ставок процентов, действующие в соответствующие периоды .

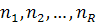На практике часто встречаются финансовые контракты, заключаемые на период, отличающийся от целого числа лет, тогда вычисляется:

1) по схеме сложных процентов: ^w+f

2) по смешанной схеме: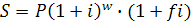

Где: w – целое число лет, 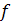- дробная часть года и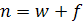

В случае ежегодного начисления процентов для лица, предоставляющего кредит:

1) Более выгодной является схема простых процентов, если срок ссуды менее 1 года (проценты начисляются однократно в конце периода).

2) Более выгодной является схема сложных процентов, если срок ссуды превышает 1 год (проценты начисляются ежегодно).

3) Обе схемы дают одинаковые результаты при продолжительности периода 1 год и однократном начислении процентов.

Сложная учетная ставка. Сложный процент начисляется в момент заключения финансового соглашения, в этом случае осуществляется операция дисконтирования и применяется сложная учетная ставка.

Если долговое обязательство продается за один год до срока, тогда продавец получит сумму: ,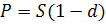

Если 2 года: ,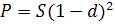

Если n-лет до срока, тогда: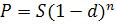

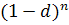– дисконтный множитель; – дисконт

Если срок n, осуществляющийся дисконтированием не является целым числом, то возможны следующие методы определения стоимости учтенного на n-лет капитала:

1) Использование сложной схемы: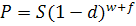

2) Использование смешанной схемы:

w – целое число лет; f – дробная часть года;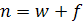

Для лица, осуществляющего дисконтирование:

1) Более выгодно дисконтирование по сложной процентной ставке, если срок учета более года.

2) Более выгодно дисконтирование по простой учетной ставке, если срок учета превышает 1 год.

3) Дисконтирование в обоих случаях дает один и тот же результат, если срок учета равен 1 году.

Дата добавления: 2014-12-07