Распределение Бозе-Эйнштейна. Теоретические сведения

Частицы, которые описываются симметричной волновой функцией (2.12), имеют целый спин и называются бозонами. Бозонами являются все частицы-переносчики взаимодействия: фотон (спин ), гравитон (спин ), -мезоны (спин ). Числа заполнения квантовых состояний при симметричных волновых функциях ничем не ограничены и могут иметь произвольные значения. Основным квантово-статистическим свойством бозонов является то, что вероятность появления бозона в некотором квантовом состоянии тем больше, чем больше таких же бозонов уже находится в этом состоянии. ИГ, состоящий из бозонов и описываемый симметричными относительно перестановок частиц волновыми функциями (2.12), называется идеальным бозе-газом.

Среднее число бозонов на уровне с энергией вычисляется по формуле:

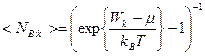
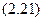
Формула (2.21) определяет распределение частиц идеального бозе-газа по энергетическим уровням и называется распределением Бозе-Эйнштейна. Химический потенциал системы бозонов .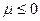

На рис. 2.5 показано распределение массивных бозонов по уровням энергии в различных областях значений энергии.

Рис. 2.5, а отвечает идеальному случаю: при 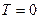К все бозоны расположены на самом нижнем энергетическом уровне – наблюдается явление конденсации Бозе-Эйнштейна.

При увеличении температуры часть бозонов переходит в более высокие энергетические состояния за счет теплового возбуждения.

Распределение бозонов, имеющих при К небольшие значения энергии, показано на рис. 2.5, б.

При больших значениях энергии частиц в правой части выражения (2.21) единицей можно пренебречь по сравнению с экспонентой: , а распределение Бозе-Эйнштейна (2.21) переходит в распределение Максвелла-Больцмана (рис. 2.5, в, г), определяемое при заданной температуре функцией:

,

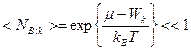(число бозонов, имеющих высокие энергии, очень мало по сравнению с числом возможных состояний) причем множитель является нормировочным (сравните с формулами (1.4) – (1.7)) и определяется условием нормировки.

Для системы бозе-газа безмассовых частиц, например, фотонов[7] или фононов, химический потенциал равен нулю, так как в систему, содержащую 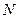таких частиц, всегда можно добавить 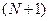-ую частицу с исчезающе малой (в пределе – нулевой) энергией, поэтому формула (2.21) для распределения Бозе-Эйнштейна принимает вид:

.

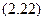
Как следует из (2.22) при 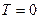K газ безмассовых бозонов перестает существовать [1].

Дата добавления: 2014-12-08