Распределение Ферми-Дирака. Применение распределения Ферми-Дирака к электронному газу в металлах. Теоретические сведения

Для системы частиц с полуцелым спином – фермионов, - описывающейся антисимметричными волновыми функциями (2.13), справедлив принцип запрета Паули: в каждом квантовом состоянии может находиться одновременно не более одной частицы.

Элементарные частицы вещества, например, электроны, нуклоны (протоны и нейтроны) и кварки имеют спин 1/2, то есть являются фермионами.

При квантовом описании изменение энергии квантовой частицы отвечает ее переходу с одного энергетического уровня на другой. Поэтому каждый квантовый уровень в квантовой статистике считается: 1) подсистемой квантовой системы; 2) системой с переменным числом частиц - открытой системой. В статистическом и термодинамическом описании открытых (например, химических, биологических) систем важную роль играет химический потенциал. Химический потенциал 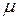при большом числе частиц в системе можно понимать как минимальное приращение внутренней энергии теплоизолированной системы с неизменным объемом при добавлении одной частицы.

С общих позиций статистической физики химическим потенциалом системы фермионов является энергия Ферми. Энергия Ферми – значение энергии уровня Ферми. Уровень Ферми при любой температуре определяется как энергетический уровень, вероятность заполнения которого равна 0,5: .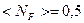

Среднее число фермионов на уровне с энергией – среднее число заполнения (вероятность заполнения уровня) – в термодинамическом равновесии вычисляется по формуле:

,

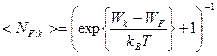где – энергия Ферми.

Формула (2.14) определяет функцию распределения ИГ фермионов – идеального ферми-газа – по состояниям и называется распределением Ферми-Дирака.

Температура Ферми (температура вырождения) – теоретическое понятие, средняя энергия фермионов, расположенных на уровне Ферми. Температура Ферми определяется отношением: . При температурах, бóльших температуры Ферми, ферми-газ описывается распределением Максвелла-Больцмана (квантовые свойства частиц становятся несущественными).

Рассмотрим газ обобществленных электронов в твердом металлическом образце. Аппроксимируя периодически меняющуюся потенциальную энергию обобществленного электрона в кристалле некоторым средним постоянным значением, металлический образец можно представить как прямоугольную потенциальную яму для электронов проводимости (рис. 2.2). С точки зрения зонной теории твердых тел эта потенциальная яма является одной из разрешенных энергетических зон – зоной проводимости. Образование таких энергетических зон происходит вследствие взаимодействия между атомами в кристалле. Взаимодействие приводит к изменению энергии атомов. В результате каждый атомарный энергетический уровень расщепляется на множество близко расположенных подуровней, которые и образуют разрешенную энергетическую зону. Для простых атомов число подуровней в зоне равно числу атомов в кристалле.

Электроны имеют спин . Следовательно, каждому энергетическому уровню ямы отвечает квантовых состояния, т. е. на каждом уровне может разместиться 0, 1 или 2 электрона. Поэтому при 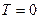K электроны будут последовательно заполнять, энергетические уровни, начиная с нижнего, по 2 электрона с противоположными направлениями спина на каждом. На последнем (самом верхнем) энергетическом уровне разместятся 1 или 2 электрона. Этот, «пограничный» между заполненными и пустыми состояниями, уровень и есть уровень Ферми при 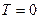K. Поэтому энергия Ферми, отсчитываемая от дна потенциальной ямы, при 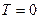K является максимальной кинетической энергией электронов в металле. Величины и определяют соответственно максимальную величину импульса и скорости фермионов при 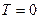К и называются ферми-импульсом и ферми-скоростью ( – масса фермиона).

На рис. 2.2 - 2.4 показано распределение электронов проводимости в металле по уровням энергии в различных областях значений энергии.

На рис. 2.2 показано распределение электронов по уровням энергии при 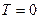К.

При увеличении температуры часть электронов, лежащих ниже уровня Ферми, переходит в более высокие энергетические состояния за счет теплового возбуждения, освобождая состояния, лежащие ниже уровня Ферми. Тепловое возбуждение даже при высоких температурах затрагивает только небольшую часть электронов проводимости в интервале энергий 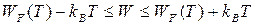. Подавляющая часть электронов остается совершенно нечувствительной к изменениям температуры. Поэтому, например, при обычных температурах электроны практически не дают вклад в теплоемкость кристалла.

При 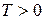К в области энергий 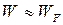распределение электронов проводимости по уровням будет иметь вид, показанный на рис. 2.3.

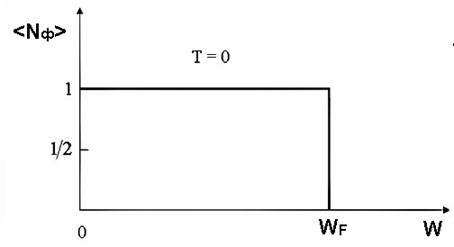
Рис. 2.2. Распределение электронов проводимости при К

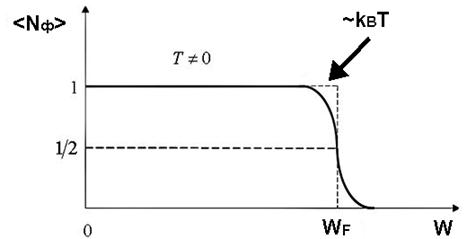
Рис. 2.3. Распределение электронов проводимости при К вблизи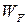

В области высоких энергий в правой части выражения (2.14) единицей можно пренебречь по сравнению с экспонентой: , а распределение Ферми-Дирака (2.14) переходит в классическое распределение Максвелла-Больцмана (рис. 2.4), определяемое при заданной температуре функцией:

(число фермионов, имеющих высокие энергии, очень мало по сравнению с числом возможных состояний), причем множитель 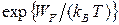является нормировочным (сравните с формулой (1.4)). Однако в металлах температура Ферми имеет порядок K и, следовательно, много больше температуры плавления: 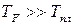. Поэтому газ электронов проводимости в металлах при любых температурах описывается распределением Ферми-Дирака.

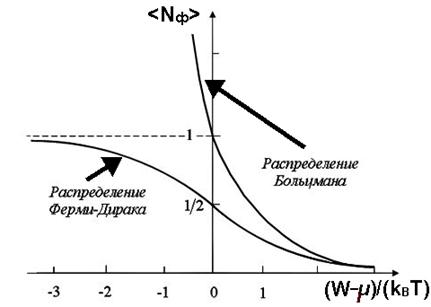
Рис. 2.4. Распределение электронов проводимости при 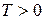К в области

высоких энергий

В соответствии с формулами (2.10), (2.11), (2.14) с учетом значения спина распределение электронов проводимости в металле по энергиям задается произведением статистического веса состояния с энергией 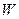на среднее число частиц в этом состоянии и определяет число электронов в объеме 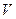с энергией в интервале от 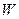до (энергия отсчитывается от дна зоны проводимости):

.

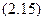
При 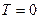K распределение Ферми-Дирака (2.14) для уровней с энергиями становится равным единице, поэтому формула (2.15) упрощается и принимает вид:

.

Если система фермионов является закрытой (нет обмена частицами с окружающей средой), то распределение Ферми-Дирака нормировано требованием сохранения полного числа фермионов. Это требование приводит к следующему выражению для энергии Ферми:

,

где 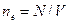– концентрация электронов проводимости в металлическом образце. 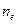вычисляется как произведение концентрации атомов и среднего числа свободных электронов, приходящихся на один атом вещества[6].

Полная энергия электронного газа в металле вычисляется по формуле:

,

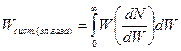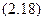
где выражение 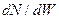определяется в общем случае по соотношению (2.15), а при 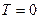К – по соотношению (2.16).

Поэтому средняя энергия электрона при 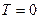К принимает значение:

.

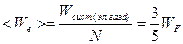Несмотря на то, что газ электронов проводимости в металле не классический, а квантовый, соотношение, связывающее давление этого ферми-газа и среднюю энергию электронов (основное уравнение молекулярно-кинетической теории ИГ) такое же, как и для классического ИГ:

.

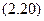
Как и классические распределения, распределение Ферми-Дирака монотонно. Поэтому при близких значениях пределов интегрирования интегралы вида (2.18) достаточно точно вычисляются путем умножения разности пределов интегрирования на значение подынтегральной функции от арифметического среднего пределов интегрирования (см. разд. 1.2 и 1.4.).

Дата добавления: 2014-12-08