
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Распределение Максвелла. Теоретические сведения
|
|
|
|
Найдем функцию распределения для импульса частицы ИГ.
Интегралы по компонентам импульса в правой части равенства (1.6) разделяются и вычисляются с помощью табличного интеграла [2]:
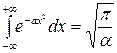 .
. 
Тройное интегрирование в условии нормировки  (вероятность найти частицу хоть с каким-нибудь импульсом равна единице) дает значение
(вероятность найти частицу хоть с каким-нибудь импульсом равна единице) дает значение  , а формула (1.6) принимает вид:
, а формула (1.6) принимает вид:
 .
. 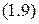
Используя выражение  , можно перейти от импульсов к скоростям и получить распределение вероятности для скорости:
, можно перейти от импульсов к скоростям и получить распределение вероятности для скорости:
 .
. 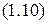
Функция распределения по скоростям классических нерелятивистских частиц физической системы, находящейся в статистическом равновесии, задаваемая формулой
 ,
, 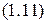
называется распределением Максвелла по проекциям скорости. Распределение Максвелла (1.11) определяет вероятное число частиц ИГ, компоненты скоростей которых лежат в интервалах от  до
до  , от
, от  до
до  , от
, от  до
до  .
.
Отсюда можно найти функцию распределения для модуля скорости частиц ИГ, которая называется распределением Максвелла по модулю скорости и задается формулой:
 .
. 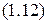
Она позволяет определить число молекул в объеме  , занимаемом ИГ, модуль скорости которых лежит в интервале значений от
, занимаемом ИГ, модуль скорости которых лежит в интервале значений от  до
до 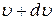 :
:
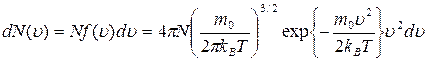

где 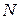 – полное число частиц ИГ.
– полное число частиц ИГ.
Чтобы найти среднее число частиц  , модули скоростей которых лежат в интервале значений от
, модули скоростей которых лежат в интервале значений от 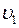 до
до  , нужно проинтегрировать функцию (1.13) в заданных пределах[1]:
, нужно проинтегрировать функцию (1.13) в заданных пределах[1]:
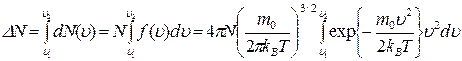 .
. 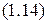
Вероятность обнаружения, или, другими словами, относительное число частиц ИГ, модуль скорости которых лежит в интервале значений от  до
до 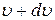 , равна:
, равна:
 .
. 
Вероятность обнаружения (относительное число) частиц ИГ, модуль скорости которых принимает значение в интервале от 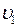 до
до  , находится по формуле:
, находится по формуле:
 .
. 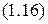
Значение модуля скорости, при котором распределение Максвелла (1.12) максимально, называется наиболее вероятной скоростью. Наиболее вероятная скорость  .
.
С помощью распределения Максвелла можно найти среднее значение любой функции, зависящей от скорости частицы. Например, среднее значение модуля скорости и среднеквадратичная скорость соответственно равны:  и
и  .
.
Для решения задач на распределение Максвелла в дополнение к интегралу (1.8) понадобятся следующие интегралы [2]:
 ;
;  ;
;  .
.
Кроме того, с учетом свойства монотонности подынтегральной функции значение интеграла (1.14) (и подобных ему) при близких значениях пределов интегрирования 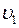 и
и  (
(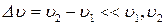 ) достаточно точно вычисляется по приближенной формуле:
) достаточно точно вычисляется по приближенной формуле:  , где
, где  – значение функции распределения Максвелла (1.12) при
– значение функции распределения Максвелла (1.12) при 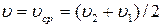 .
.
|
|
|
|
|
Дата добавления: 2014-12-08; Просмотров: 719; Нарушение авторских прав?; Мы поможем в написании вашей работы!