Уравнение движения артиллерийского оружия при стрельбе

4.4.1. Вывод уравнения движения оружия на амортизаторе

при стрельбе

С целью упрощения вывода уравнения движения оружия вводятся следующие условия:

Рисунок 4.14. Силы, действующие на корпус оружия, имеющего АСО с витой пружиной

1. Центр масс оружия находится на линии оси канала ствола.

2. Все силы, действующие при стрельбе на корпус оружия приложены в центре масс.

На рисунках 4.14 и 4.15 показаны силы, действующие на корпус оружия при стрельбе.

Начало системы координат OXY расположены в центре масс, которое он занимает до начала стрельбы из оружия.

Рисунок 4.15. Силы, действующего на корпус оружия, имеющего АСО с кольцевой пружиной

В соответствии с принципом Даламбера, условие равновесия сил, действующих на корпус оружия, запишется в виде:

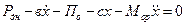, (АСО с витой пружиной);

, (АСО с кольцевой пружиной);

где М_ор – масса оружия;

x, 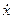, – перемещение, скорость и ускорение перемещения оружия при стрельбе, соответственно;

М_ор – сила инерции, действующая на корпус оружия.

После перегруппировки членов получим

, (4.10)

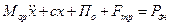. (4.11)

Выражения (4.10), (4.11) являются линейными неоднородными дифференциальными уравнениями второго порядка.

4.4.2. Решение уравнения движения оружия на амортизаторе

при стрельбе

Воспользовавшись выражением (4.10), приведем решение уравнения движения оружия при стрельбе.

С целью исключения громоздких выражений и, следовательно, повышения наглядности решения, приведем уравнение (4.10) к безразмерному виду.

Как известно из теории внутренней баллистики импульс силы давления пороховых газов Р_дн определяется из выражения

, причем P_дн= P_дн(t). (4.12)

Умножим каждый член уравнения (4.10) на отношение :

. (4.13)

Введем следующие безразмерные величины:

- безразмерное время ; (4.14)

- безразмерное линейное перемещение оружия ; (4.15)

откуда ; (4.16)

- безразмерную силу давления пороховых газов с учетом усилия предварительного поджатия пружины амортизатора

. (4.17)

Учитывая, что 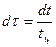, продифференцируем по τ выражение (4.15)

,

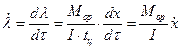откуда . (4.18)

Находим вторую производную по τ:

,

откуда . (4.19)

Подставляя (4.16), (4.17), (4.18), (4.19) в (4.13) получим

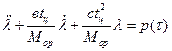. (4.20)

Введем обозначение

– это приведенная собственная частота колебаний оружия при стрельбе;

Из этого выражения получим .

С учетом последнего равенства, второй член в (4.20) можно записать

.

Обозначим 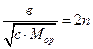, где n – коэффициент затухания.

С учетом введенных обозначений перепишем выражение (4.20)

(4.21)

Выражение (4.21) – это неоднородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами.

В соответствии с понятиями теории механических колебаний уравнение (4.21) описывает вынужденные колебания материальной точки (то есть центра масс оружия), находящейся под воздействием возмущающей силы Р(τ), восстанавливающей силы а²λ и силы сопротивления .

Если закон изменения возмущающей силы Р(τ) известен, то решение уравнения (4.21) традиционно и складывается из общего решения соответствующего однородного линейного уравнения

(4.22)

и частного решения, которое выбирается по виду правой части уравнения (4.21), либо определяется несложным и нетрудоемким подбором.

Общее решение (4.22), как известно, имеет вид

, (4.23)

где С₁, С₂ – произвольные постоянные;

Z₁, Z₂ – корни характеристического уравнения;

τ – безразмерное время.

Характеристическое уравнение имеет вид .

Выражения для Z₁, Z₂ зависят от значения n. Из трех возможных случаев: (n<1, n=1, n>1), для авиационного артиллерийского оружия, закрепленного на лафете, как показывает практика, имеет место неравенство n<1. В этом случае корни характеристического уравнения комплексные числа

;

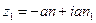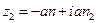, (4.24)

где .

В реальности при стрельбе из авиационного артиллерийского оружия закон изменения возмущающей силы (Р(τ)) не известен, поэтому отыскание частного решения представляет значительные трудности. В этом случае применяется метод предложенный Лагранжем и называемый методом вариации постоянных.

В соответствии с этим методом общее решение однородного линейного уравнения (4.22) записывается в виде аналогичном (4.2.3), но С₁, С₂ считаются уже не произвольными постоянными, а функциями независимого переменного τ.

Для их определения необходимо иметь два дополнительных уравнения. Эти уравнения можно задать произвольно, но чаще они задаются таким образом, чтобы выражения для производных от λ имели наиболее простой вид.

Дифференцируем (4.2.3) по τ

(4.25)

где , , .

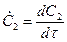В качестве первого из упомянутых выше дополнительных уравнений возьмем уравнение, которое получится, если два последних члена правой части выражения (4.25) приравнять к нулю

. (4.26)

С учетом (4.26) выражение для примет вид

. (4.27)

Дифференцируем (4.27) по τ

(4.28)

Подставим выражение (4.23), (4.27), (4.28) в уравнение (4.21) и, после преобразований, получим

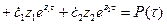. (4.29)

Заметим, что выражения

;

,

так как это результат подстановки в левую часть уравнения (4.22) его решений.

В результате получаем второе дополнительное уравнение для определения С₁, С₂,

. (4.30)

Разрешая систему из двух неоднородных линейных уравнений (4.26) и (4.30) с двумя неизвестными 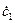, , получим

; (4.31)

.

Интегрируя выражение (4.31), находим

;

,

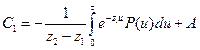где А, В – комплексные постоянные.

После подстановки найденных значений С₁, С₂ в (4.23) найдем общее решение исходного уравнения (4.21)

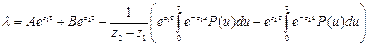. (4.32)

Как видно, выражение (4.32), являясь решением уравнения (4.21), фактически содержит общее решение уравнения (4.22) – первые два слагаемые и частное решение неоднородного уравнения (4.21) – вторые два слагаемые.

Подставим выражения (4.24) и, проведя необходимые преобразования, окончательно получим выражение для, интересующего нас, действительного решения уравнения (4.21)

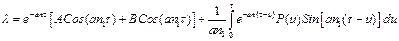. (4.33)

Полученное выражение позволяет исследовать движение авиационного артиллерийского оружия на амортизаторе при стрельбе очередью и дать рекомендации по выбору конструкции и параметров пружины амортизатора с целью обеспечения высокой надежности работы автоматики оружия, повышению эффективности его боевого применения и снижению силового воздействия на лафет установки.

В качестве примера, на рисунке 4.16 представлен график перемещения корпуса пушки ГШ-30 при стрельбе очередью.

Рисунок 4.16. Перемещение пушки ГШ-30 при стрельбе

Как видно из графика, наибольшее перемещение оружие имеет после первых двух выстрелов. Далее колебания стабилизируются и происходят относительно точки, отстоящей от исходного положения в сторону отката на расстоянии приблизительно равное 0,8 см.

Примерно такой же характер колебаний при стрельбе имеют и другие образцы ААО.

Дата добавления: 2014-12-27