Методика определения средней силы отдачи амортизатора

При разработке методики определения средней силы отдачи (П_ср) амортизатора учитывается условия, которые были приняты в § 4.3 при выводе уравнения движения оружия при стрельбе. Дополнительно принимается условие, что сумма сил из выражения (4.10) или сумма сил 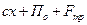из (4.11) равны некоторому среднему значению П_ср, то есть

или .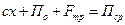

Причем считается, что П_ср = const.

С учетом сказанного, уравнение движения оружия на АСО при стрельбе принимает вид

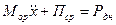. (4.35)

Дважды проинтегрируем выражение (4.35). С учетом начальных условий t =0, x =0, 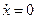, получаем выражение, позволяющее определить перемещение оружия в конце очереди из q выстрелов.

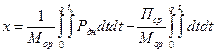. (4.36)

Первый интеграл в (4.36) выражает перемещение (откат) оружия только под действием силы давления (P_дн) пороховых газов на дно запертой в патроннике гильзы. Второй интеграл выражает перемещение (накат) оружия только под действием средней силы отдачи (П_ср) амортизатора. Остальные силы принимаются равными нулю.

Вычисление интеграла 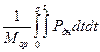вызывает большие трудности, поскольку точно не определена зависимость P_дн= P_дн(t). По этой причине указанный интеграл будем вычислять приближенно, как сумму перемещений после каждого выстрела при отсутствии сил сопротивления.

Отметим, что при относительно большом значении времени t_ц (то есть низком темпе стрельбы) оружие после выстрела успевает достичь максимальной скорости (V_m) отката. Следующий выстрел увеличивает скорость отката на V_m. Значение V_m можно определить, воспользовавшись известными законами внутренней баллистики. Таким образом, при низком темпе стрельбы перемещение оружия определяется выражением

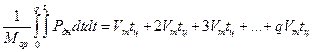. (4.37)

Однако, при высоком темпе стрельбы, следовательно, малом значении t_ц, оружие не успевает к следующему выстрелу достичь максимальной скорости отката. Считается, что оружие до следующего выстрела перемещается со скоростью V_ср, которая меньше V_m. Чтобы связать скорость V_ср со скоростью V_m, которую можно теоретически вычислит, вводится коэффициент α <1. Значение этого коэффициента зависит от отношения времени действия силы P_дн к времени t_ц.

Например, для пушек калибра 23 мм: α =0,97…0,985, при Т =1000 в/м;

α =0,84…0,85, при Т =6000 в/м.

Учитывая сказанное выше, перепишем выражение (4.37)

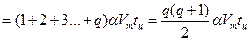. (4.38)

Второй интеграл в выражении (4.36) можно записать в виде

. (4.39)

С учетом (4.38), (4.39) перемещение оружия в конце очереди из q выстрелов определяется выражением

. (4.40)

Предположим, что к концу q -го цикла автоматики оружие возвращается в исходное положение, то есть x =0. В этом случае схема амортизации определяется как

.

Учитывая сказанное, получаем равенство

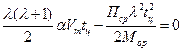. (4.41)

Из (4.41) находим выражение для П_ср

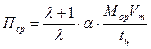. (4.42)

В соответствии с обозначениями и терминологией, принятыми в теории внутренней баллистики, – это полный импульс силы давления пороховых газов с учетом периода последействия. Окончательно выражение для определения средней силы отдачи амортизатора имеет вид

, (4.43)

где Т – темп стрельбы в выстр/мин.

В качестве примера, рассчитаем среднюю силу отдачи амортизатора пушки ГШ-30 при следующих исходных данных: λ =1; α =0,91; I_δ =496,4 Нс; Т =3000 выстр/ми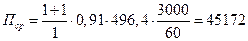н.

Н.

Анализ выражения (4.43) показывает, что переход от полуцикловой схемы амортизации к одноцикловой дает возможность уменьшить силу отдачи амортизатора в 1,5 раза (при λ =0,5, =3, а при λ =1, =2, следовательно, 3:2=1,5).

Переход от одноцикловой схемы к двухцикловой обеспечивает снижение силы отдачи амортизатора в 1,33 раза (при λ =2, =1,5, следовательно, 2:1,5≈1,33).

Применение более "мягких" схем амортизации на практике нецелесообразно, поскольку существенно возрастает величина отката оружия и, если оставить неизменными характеристики патронной ленты, растет вероятность ее заклинивания при подаче в автоматику оружия.

Дата добавления: 2014-12-27