Оптимизация сетевого графика

Одна из задач при построении сетевого графика, как отмечалось, – максимальное сокращение длительности критического пути и, соответственно, всей разработки. Оптимальным является случай, когда все полные пути – критические. Это уменьшает время выполнения проекта, но увеличивает напряженность на всех работах. Сокращение продолжительности критического пути в том случае, когда его расчетная величина превышает заданное значение, достигается либо привлечением дополнительных ресурсов, либо в ходе оптимизации графика за счет изменения топологии сети, состава и содержания работ, при этом проверяется структура сети с целью устранения излишних связей, ищется возможность организации параллельного выполнения работ, до этого выполняемых последовательно, а так же рассматривается возможность использования ресурсов работ подкритического пути (имеющих резервы времени) на работах критического пути.

Оптимизация графика путем использования трудовых ресурсов работ подкритического пути на работах критического пути применяется, когда эти работы совпадают во времени и имеет место соответствие переводимых работников по специализации и квалификации. На рисунке 5 продолжительность работ подкритического и критического пути составляют, соответственно, t_ij и t^кр_ij.Эти работы параллельны. Работа подкритического пути имеет полный R_nij и свободный R_cij резервы времени, т.е. имеется возможность увеличения ее продолжительности в

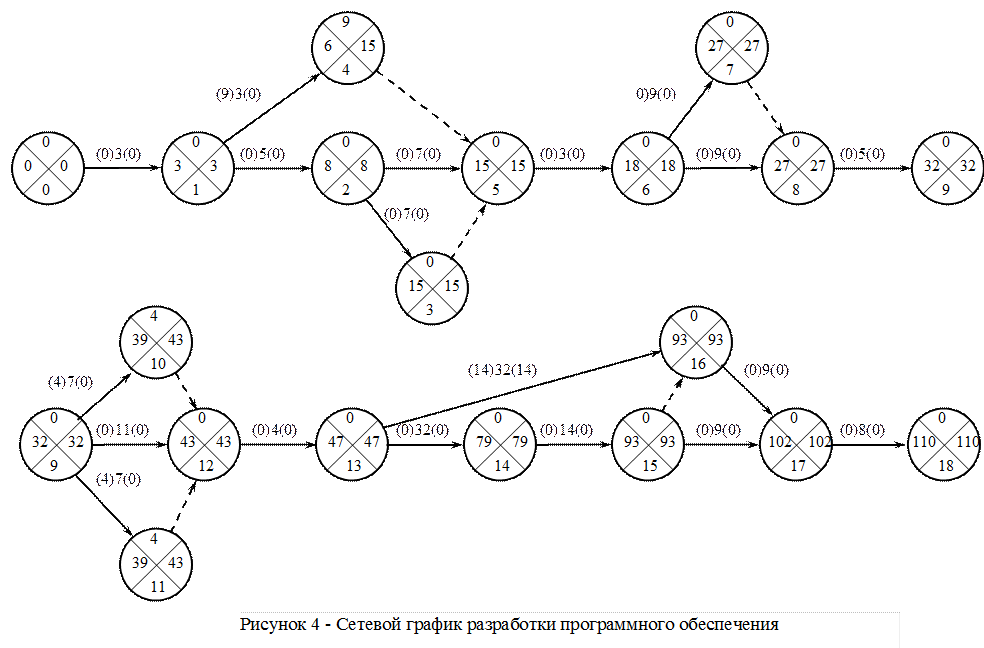
пределах этих резервов времени. Предполагается, что количество работников на этой работе не менее двух.

При переводе работников продолжительность работ подкритического пути увеличивается, а работ критического пути, соответственно, уменьшается. Обычно рекомендуется использовать до 80%, и более, свободного резерва времени работ подкритического пути.

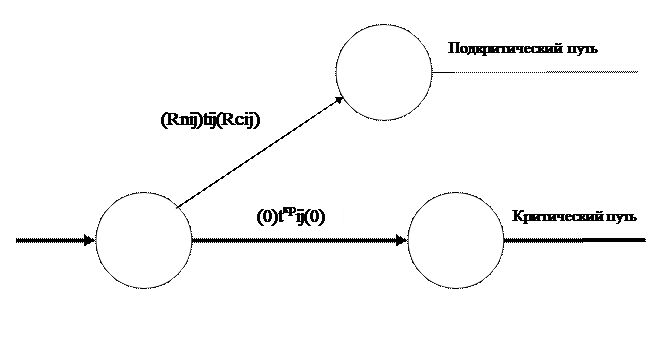
Рисунок 5 – Элемент сетевого графика до оптимизации

Если допустить увеличение продолжительности работы подкритического пути на величину свободного резерва времени R_cij, то расчетное количество работников, которое можно при этом перевести на работу критического пути, составит:

х = Wij – ,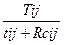

где Wij – количество работников на работе подкритического пути до оптимизации;

Тij – трудоемкость работы подкритического пути;

tij - продолжительность работы подкритического пути до оптимизации;

Rcij - величина используемого резерва времени (в данном случае свободного резерва времени).

Расчетное количество переводимых работников х округляется до целого значения х *.

Далее устанавливается окончательная продолжительность работ после перевода сотрудников:

t_ij* = ,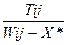

t^кр*_ij = ,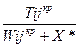

где t_ij* и t^кр*_ij - новые продолжительности работ соответственно подкритического и критического пути после оптимизации;

Т_ij^кр – трудоемкость работы критического пути.

После использования всех возможных способов оптимизации графика делается перерасчет его параметров и определяется новая продолжительность критического пути.

Дата добавления: 2014-12-27