
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Выбор компоновки
|
|
|
|
С подвижной стойкой
Из всего множества возможных для заданных движений вариантов базовых компоновок необходимо выбрать один, наилучший для конструируемого станка и конкретных условий его использования на производстве. Некоторые критерии для отбора вариантов могут быть обусловлены в формализованном виде и окончательно сформулированы в виде условной записи. Если станок предназначен для обработки крупных деталей, то нежелательно эту деталь вместе с подвижным узлом перемещать вертикально. Пользуясь символикой алгебры логики, это условие можно записать таким образом:
М 1 = 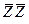 O
O 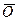 +
+ 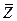 O
O 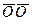 + О
+ О 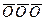 , (5)
, (5)
где 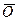 ,
, 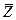 — читаются как подвижный узел (не О) и как горизонтально-подвижный узел (не Z).
— читаются как подвижный узел (не О) и как горизонтально-подвижный узел (не Z).
Условию (5) удовлетворяет лишь часть вариантов множества (рис. 8, а), а именно те, которые входят в определенное подмножество (рис. 8, б). Если тяжелую деталь следует обработать с высокой точностью, то желательно, чтобы эта деталь или была совсем неподвижной, или имела бы только одно горизонтальное перемещение. Это условие можно записать таким образом:
М 2 = 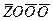 +
+ 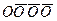 , (6)
, (6)
и при этом возможными остаются также лишь определенные варианты (рис. 8, в). Рассмотренное условие иногда целесообразно также для станков, встраиваемых в автоматическую линию или автоматический участок.
Можно также поставить условие, чтобы горизонтально-подвижные узлы примыкали к неподвижному. При этом не будет изменения консольно приложенной нагрузки от собственной массы и соответствующих погрешностей обработки. Данное условие формально записывают в виде
М 3 = 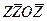 +
+ 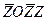 (7)
(7)
и характеризуют своим подмножеством вариантов (рис. 8, г).
Совместное выполнение трех условий (5) — (7) может быть записано в форме матрицы для использования способа поразрядной конъюнкции (с. 40).
Знак Ф соответствует нуль-множеству, которое выражает противоречие условий.
Итак, совместное выполнение поставленных условий приводит к тому, что из всего возможного множества компоновок (см. рис. 8, а) оказываются пригодными лишь два варианта, изображенные на рис. 10, а, б.
| М 1 | — | 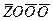
| + 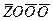
| + 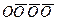
|
| М 2 | — | — | 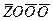
| + 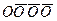
|
| М 3 | — | 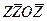
| + 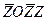
| — |
| Ф | Ф | XOYZ | Ф | |
| YOXZ |
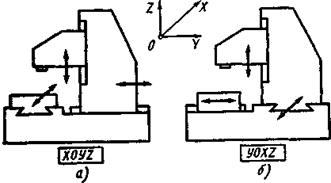
Рис. 10. Варианты компоновок, удовлетворяющие
совокупности ограничивающих, условий
Из двух оставшихся возможных вариантов базовой компоновки выбирают лучший вариант по различным дополнительным соображениям. Так, например, в зависимости от решения вопросов автоматизации загрузки-выгрузки деталей на рабочую позицию может оказаться предпочтительным любой из оставшихся вариантов. Тщательный анализ жесткости всей несущей системы может привести к окончательному выбору варианта, обеспечивающего достаточную жесткость. Известно, например, что замкнутые, несущие системы (портального типа) могут существенно повысить статическую жесткость и виброустойчивость по сравнению с той же компоновкой, но не замкнутого вида.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 687; Нарушение авторских прав?; Мы поможем в написании вашей работы!