Оптимизация проектных решений

Как уже отмечалось, важнейшей предпосылкой автома­тизации процесса проектирования является возможность нахожде­ния оптимального варианта технической системы. Техническая система одной структуры может иметь несколько допустимых решений за счет различных значений ее параметров. В этом случае возможен такой набор значений параметров, который обеспечивает оптимальное решение. Процесс поиска решения назы­вают параметрической оптимизацией. В дальнейшем при рассмо­трении различных аспектов процесса оптимизации всегда имеется в виду параметрическая оптимизация, а структура системы считается заданной. Используя параметрическую оптимизацию, можно про­водить оценку различных структур системы, сравнивая между собой их оптимальные варианты. Синтез вариантов системы осуществляется с помощью математической модели, представляющей собой совокуп­ность формул, позволяющих определить все интересующие нас про­ектные характеристики технической системы. В общем случае эта модель выглядит следующим образом.

Имеется вектор X = (х ₁, х ₂,..., х_n) независимых внутренних параметров, значения которых однозначно определяют все харак­теристики изделия, в том числе значения целевой функции F и функ­ций ограничений R ₁, R ₂,..., R_m. Таким образом, целевая функция и функции ограничений зависят от внутренних параметров. Эта зависимость в общем случае нелинейна. Независимые параметры — это обычно размеры изделия или характеристики его элементов. Так, для шпиндельного узла независимыми параметрами могут быть диаметры опорной шейки, межопорной части, длина консоли, же­сткость подшипника и т. д.

В процессе оптимизации часть независимых внутренних пара­метров подвергается изменениям в определенных пределах. Такие параметры называют управляемыми, а пределы их изменений — параметрическими ограничениями. Формальная постановка задачи параметрической оптимизации сводится к нахождению таких зна­чений независимых параметров, при которых целевая функция F = F (X) достигает своего минимума при

x_j ≥ 0, j = 1, 2,...., n (1)

и

R_i (X) ≤ 0, i = 1,2,..., m; m ≤ n, или m ≥ n. (2)

К такой постановке может быть приведена любая реальная за­дача. Действительно, если по смыслу задачи требуется максимизация целевой функции, то, умножая ее на минус единицу, получаем тре­буемую форму.

Геометрическая интерпретация постановки задачи оптимизации для случая двух независимых переменных показана на рис. 3, где нанесены линии постоянного уровня целевой функции F (х ₁, х ₂) и функций ограничений R_i (x ₁, x ₂), i = 1, 2, 3.

В каждой точке одной такой линии целевая функция (функция ограничений) имеет одно и то же постоянное значение. Уравнением линии постоянного уровня является выражение

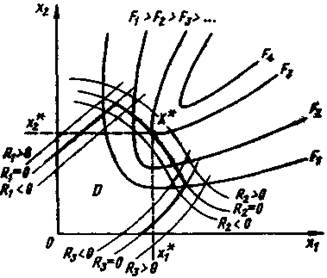
Рис. 3. Геометрическая интерпретация задачи

оптимизации

F (x ₁, x ₂) = а [или R_i (x ₁, х ₂) = а_i ],

где, а = const. Задавая различные значения постоянной а, получим семейство линий постоянного уровня.

Условия (1) и (2) выделяют область D — область допу­стимых решений. Минимум целевой функции в данном случае на­ходится на границе области D в точке X^* = (х_i ^*, х ₂^*). Такой минимум называется условным, а задача его нахождения — условной оптими­зацией, в отличие от безусловной оптимизации, когда ищется минимум целевой функции в отсутствии функций ограничений. В технических задачах ограничения имеются практически всегда.

Критерии оптимальности. Перейдем теперь к рассмотрению клю­чевого вопроса решения задач оптимизации — выбору целевой функции. Напомним, что це­левая функция позволяет получить количественную оценку качества проектируе­мого изделия. Такой оцен­кой, в рамках принятой нами модели, может быть вектор выходных характеристик

Y = (y ₁, у ₂,..., y_s),

который, как отмечалось, однозначно определяется значениями независимых пара­метров x_j.

Отдельные выходные ха­рактеристики (условимся называть их частными кри­териями) y_k, k = 1, 2,..., s — это, по существу, тех­нико-экономические показатели изделия. Например, применительно к станку это могут быть его производительность, точность, материалоемкость и т. п. Обычно предельно допустимые значения выходных характеристик содержатся в техническом задании на проектирова­ние. Обозначим эти значения через y_k ^т.з.. Тогда выражение

y_k - y_k ^т.з ≤ 0 (3)

можно назвать условием работоспособности.

Приведенная форма этого условия может быть реализована для любых характеристик, так как когда по смыслу задачи требуется обратное неравенство, оно может быть заменено неравенством вида (3), если вместо y_k и y_k ^т.з взять их обратные величины.

Степень выполнения требований технического задания может быть оценена выражением

.

Критерии Δ y_k не противоречат принятому условию минимизации целевой функции, а их безразмерная форма позволяет сравнивать между собой характеристики разной физической природы. Основные трудности в использовании критериев y_k или Δ y_k для оценки проекта состоят в том, что эти критерии не являются независимыми, так как все они — функции внутренних параметров.

Среди этих критериев всегда находятся такие, улучшение кото­рых приводит к ухудшению других. Такие критерии называются конфликтными. Наличие конфликтных критериев не позволяет ставить целью одновременное улучшение всех выходных характе­ристик изделия, требуется поиск компромиссного решения. Отметим, что такое решение в принципе не может быть формализовано, а, сле­довательно, и автоматизировано, так как цель — прерогатива че­ловека и его деятельности.

Задачи, в которых качество изделия требуется оценивать и улуч­шать по нескольким характеристикам одновременно, называют за­дачами многокритериальной оптимизации. К этой категории отно­сятся практически все задачи, с которыми сталкивается конструк­тор-станкостроитель. Рассмотрим некоторые подходы к формирова­нию целевой функции в многокритериальных задачах. Самым про­стым подходом является такой, когда из набора частных критериев выбирают главный, который принимают в качестве целевой функ­ции. В этом случае оптимальное решение имеет большой запас по выбранному критерию и полное отсутствие запасов по остальным. В станкостроении использование частного критерия как целевой функции можно рекомендовать только при проектировании уни­кального оборудования, когда получение требуемого качества (на­пример, сверхточный станок и т. п.) окупает почти любые издержки.

Наиболее распространенным подходом в многокритериальных задачах является формирование аддитивного критерия. Целевая функция в этом случае имеет вид

,

где C_k — так называемые весовые коэффициенты, определяющие степень влияния каждого частного критерия на целевую функцию. Их численные значения находят с помощью экспертных оценок. Обычно полагают

.

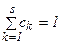Основной недостаток аддитивного критерия — отсутствие объек­тивной достоверности значений весовых коэффициентов. Если при проектировании технического объекта имеется возможность полно и достоверно оценить произведенные затраты, то их также можно использовать в качестве целевой функции. Более того, можно утвер­ждать, что минимизация затрат — наилучший подход при проек­тировании, так как это единственный способ получения «объектив­ной» оценки такого субъективного понятия как цель. Здесь необхо­димо подробно пояснить, что имеется в виду под полным учетом затрат. Лучше всего это делать на конкретном примере. Допустим, мы проектируем станок, который должен быть встроен в автомати­ческую линию, предназначенную для изготовления деталей авто­мобильного двигателя. При сравнении различных вариантов проекта для полного учета затрат необходимо, кроме всего прочего, учесть приведенные эксплуатационные расходы в автоматической линии (они существенно зависят от надежности и ремонтопригодности кон­струкции), расходы на изготовление двигателя и в период эксплуа­тации автомобиля (на них влияет уровень качества изготовленных деталей). Как видим, полный учет затрат — дело довольно сложное и в настоящее время мало разработанное. Это обстоятельство яв­ляется основным сдерживающим фактором в применении стоимост­ного критерия в оптимизационных задачах.

Заканчивая на этом рассмотрение вопроса о выборе целевой функции, подчеркнем, что качество оптимального решения целиком зависит от того, какой критерий выбран для оценки.

Минимальное значение целевой функции может быть найдено непосредственно, если она выражена аналитически.

Обычно в технических задачах аналитические выражения для целевой функции и функций ограничений отсутствуют. Поэтому минимум целевой функции определяют, используя поисковую оптимизацию. Суть этого процесса состоит в том, что опреде­ляют последовательный ряд точек, обра­зующих траекторию в пространстве не­зависимых параметров, двигаясь вдоль которой можно достичь минимума целе­вой функции. При этом в каждой точке вычисляют значение целевой функции и проверяют условия прекращения поиска. Таким условием может быть, например, незначительное, по сравнению с предыду­щим шагом, уменьшение целевой функции.

Рассмотрим некоторые методы поиска минимума целевой функ­ции. Большинство методов разработано для случаев безусловной оптимизации, но их можно применять в задачах с ограничениями, так как существуют приемы сведения задач условной оптимизации к задачам безусловной оптимизации. Существо метода и его назва­ние определяются способом выбора направления поиска в простран­стве независимых параметров.

Самым простым методом поиска является метод полного перебора. При этом всю область D разбивают на элементарные подобласти, в каждой из которых вычисляют целевую функцию. Сравнивая по­лученные значения между собой, находят минимум целевой функ­ции. Метод наиболее удобен для задач с небольшим количе­ством независимых параметров (три-четыре) и ограниченными диапа­зонами их изменений.

Метод координатного спуска предполагает направление поиска на очередном шаге, совпадающем с направлением одной из коорди­натных осей. Другими словами, имеет место последовательная опти­мизация по каждому независимому параметру. Например, вначале осуществляется движение в направлении оси Х ₁ до тех пор, пока целевая функция уменьшается. Когда такое уменьшение прекра­щается, начинают движение в направлении оси Х ₂ и т. д. После окончания полного цикла спусков по направлениям всех независи­мых параметров вновь возвращаются к направлению Х ₁ и реализуют новый цикл. Так продолжают до тех пор, пока не находят минимум целевой функции. Траектория, соответствующая описанному алго­ритму, показана на рис. 4 для случая двух независимых пере­менных.

Рис. 4. Метод координатного спуска

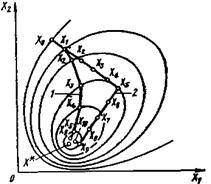Рис. 5. Метод градиента (1) и метод наискорейшего спуска (2)

В следующих двух методах — методе градиента и методе наиско­рейшего спуска — при выборе направления поиска используют информацию о градиенте целевой функции. Так как направление градиента определяет направление наиболее быстрого возрастания целевой функции, то целесообразно поиск ее минимума вести в анти­градиентном направлении. При этом метод градиента предусматривает определение этого направления в каждой точке траектории поиска, а при методе наискорейшего спуска движение в антиградиентном направлении осуществляется до тех пор, пока происходит уменьшение целевой функции. На рис. 5 изображены траектория 1 поиска по методу градиента и траектория 2 наискорейшего спуска. Сравнивая траектории 1 и 2, можно заключить, что метод наискорейшего спуска требует большего числа шагов, но при этом методе реже вычисляется градиент целевой функции.

Сведение задач условной оптимизации к безусловной может быть, выполнено, в частности, с помощью метода штрафных функций. Суть метода заключается в замене целевой функции F (X) исходной задачи на обобщенный критерий, значения которого совпадают с F (X) внутри области допустимых решений и резко возрастают вне ее. В обобщенный критерий T (X, t) вводится коэффициент штрафа t.

Минимум функции Т (X, t) стремится к минимуму функции F (X) при t → ∞. Для всех X D можно обойтись без штрафных функций, если заранее известно, что минимум лежит внутри области D. Обычно такая априорная информация отсутствует.

Метод случайного поиска реализует выбор направления поиска на каждом шаге случайным образом, например, используя таблицы случайных чисел. Так, из некоторой точки X_k переходят в точку X_{k +1}, и если при этом оказывается F (X_{k +l}) < F (X_k), то попытка счи­тается удачной и поиск продолжают из точки X_{k +l}. Если F (X_{k +1}) ≥ F (X_k), то попытка считается неудачной, и из точки находят но­вое случайное направление. Поиск прекращают после L неудачных попыток. Число попыток L задают заранее, его значение определяют из опыта решения подобных задач. Этому методу присущ тот недо­статок, что точки, в которых вычисляются значения F (X), могут распределиться неравномерно в пространстве независимых пара­метров, из-за чего определенные области этого пространства ока­жутся вне анализа.

Этот недостаток отсутствует в методе линейного программирования (ЛП-поиска). Математический аппарат метода обеспечивает формирование векторов X ₁, Х ₂ ,..., Х_N в N точках, равномерно расположенных в пространстве неза­висимых параметров. Другим важным достоинством этого метода является выработанная удобная форма анализа комплекса частных критериев в виде так называемой таблицы испытаний. Под испыта­нием здесь понимаем определение значений параметров и критериев в одной из N точек. Таким образом, общее число испытаний равно N, и для каждого из них вычисляют значения всех частных критериев. Каждому критерию в таблице испытаний отведена одна строка, в которой значения этого критерия располагают в порядке возра­стания с указанием номера испытаний. Сумма таких строк по всем частным критериям позволяет анализировать комплекс этих крите­риев при отсутствии целевой функции в явном виде, рассмотрев все возможные компромиссы.

Дата добавления: 2014-12-27