В примерах на EXCEL 3 страница

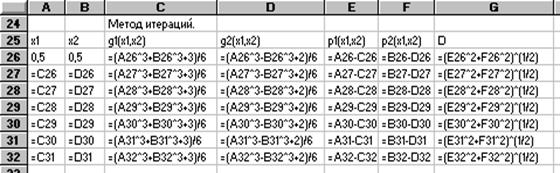
Отведем столбец А, начиная с 26 строки под значения х₁, столбец В под значения х₂, столбец С - под g₁, столбец D - под g₂, следующие три столбца под р₁,р₂ и D.

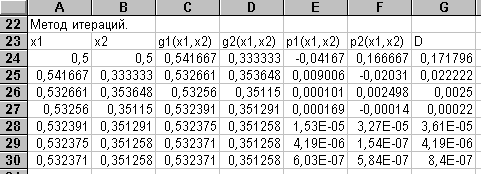
В строке 27 сформируем формулы для второй итерации, а затем скопируем их в блок А28:G32, с учетом изменений относительных адресов ячеек. В результате будем иметь заполненную таблицу

Как видно, процесс итераций сходится достаточно быстро.

4. ЧИСЛЕННЫЕ МЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ.

Одномерная задача оптимизации в общем случае формулируется следующим образом: найти значение независимой переменной Х, заданной на интервале[a,b], при котором некоторая целевая функция f(X) принимает минимальное значение. Если ставится задача нахождения максимума, например, функции g(X), то преобразованием f(X) = - g(X) она приводится к отысканию минимума f(X). Целевая функция f(X) должна быть задана в виде формулы. Если существует производная f’(X), то задача сводится к решению уравнения f’(X) = 0, например, методами, описанными в разделе 2.

Численные методы оптимизации используются тогда, когда целевая функция недифференцируема и, в общем случае, может быть не гладкой и даже непрерывной, т.е. может иметь разрывы первого рода по Дирихле.

Единственное условие, предъявляемое к целевой функции - она должна быть унимодальной на интервале [a,b], т.е. иметь на этом интервале только один минимум и не иметь ни максимумов, ни точек перегиба. Математически свойство унимодальности записывается так. Функция f(X) называется унимодальной на интервале [a,b], если на этом интервале существует такая точка Х*, что для значений Х

X₁<X₂<X*<X₃<X₄

выполняется условие

f(X₁)>f(X₂)>f(X*)<f(X₃)<f(X₄).

В этом определении очень важно, что все неравенства - строгие.

Процесс нахождения минимума унимодальной функции численными методами оптимизации, называемыми иногда методами поиска, состоит в последовательном сужении интервала [a,b] - начального интервала неопределенности - так, чтобы его длина достигала значения Е - заданной погрешности решения.

Алгоритм сужения интервала [a,b] называется стратегией поиска. Заметим, что если выбрать два любых значения Х₁ и Х₂ на интервале [a,b] и вычислить для них значения функции f(X₁) и f(X₂), то сравнивая эти значения по величине и используя свойство унимодальности, всегда можно сократить начальный интервал неопределенности, отбрасывая отрезок [a,X₁] или отрезок [X₂,b]. Таким образом, стратегии поиска отличаются правилами выбора значений Х₁ и Х₂ на интервале [a,b]. Далее будут рассмотрены три метода одномерной оптимизации.

4.1. Метод дихотомии.

Для использования метода дихотомии должно быть дано:

а) формула целевой функции f(X),

б) численные значения а - левой границы и b - правой границы начального интервала неопределенности, на котором целевая функция унимодальна,

в) численное значение Е - точности нахождения значения Х, при котором f(X) принимает минимальное значение на [a,b].

Сущность метода состоит в том, что выбираются значения Х₁ и Х₂ так, чтобы они были как можно ближе к середине интервала неопределенности с=(a+b)/2. Обычно Х₁ = с-r и Х₂ = c+r, где r = E/3 или E/4 в зависимости от точности вычислений компьютера. Таким образом, на каждой итерации отбрасывается отрезок длиной (c-r), почти равной половине интервала неопределенности. Через К итераций начальный интервал неопределенности уменьшится до длины

d = (b-a)/2^K + r(2^K - 1)/2^(K-1).

Итерации прекращаются, если d <= E.

Итак, алгоритм метода дихотомии состоит в следующем.

1) для заданных значений a и b вычисляются с=(a+b)/2, X₁ = c-E/3 и X₂=c+E/3,

2) вычисляются значения f(X₁) и f(X₂) и сравниваются между собой,

3) если f(X₁) > f(X₂), то а= X₁, иначе b= X₂,

4) если длина нового интервала d=(b-a) <=E, то вычисления останавливаются и в качестве решения можно взять любое значение Х, лежащее внутри этого интервала; в противном случае выполняется новая итерация.

Пример 4.1.

Пусть надо найти минимум функции f(X) = 2X² + e^-X. По правилам EXCEL эта функция должна быть записана так =2*Х^2 + EXP(-X), где вместо Х нужно подставить тот или иной адрес ячейки. Зададим Е= 0,0001.

Первый этап решения задачи состоит в нахождении начального интервала неопределенности, на котором функция f(X) унимодальна. С помощью EXCEL это легко сделать, протабулировав функцию f(X) в некоторых пределах, например, от -1 до 1 с шагом 0,2.

Откроем новый рабочий лист EXCEL. Поместим числовой ряд Х в блок А5:А16, оставив ячейку А4 пустой. В ячейку В4 занесем формулу =2*А4^2+EXP(-А4). Далее можно воспользоваться подпрограммой ТАБЛИЦА, вызвав ее командой меню Данные- Таблица и действуя так, как описано в примере 2.1. Как видно из таблицы, интервал неопределенности можно выбрать между а=0 и b=1.

Запрограммируем решение нашей задачи методом дихотомии в блоке А24:G37, внеся необходимые числовые значения и формулы. Для изменения значений a и b используем функцию ЕСЛИ Мастера Функций. Приведем таблицу формул в соответствующих ячейках для первых двух итераций в строках 24 и 25. Формулы для остальных строк блока копируются из 25 строки.

Адрес	Формула
A24
B24
C24	=(A24+B24)/2-0,0001/3
D24	=(A24+B24)/2+0,0001/3
E24	=2*C24^2+EXP(-C24)
F24	=2*D24^2+EXP(-D24)
G24	=B24-A24
A25	=ЕСЛИ(E24>F24; C24; A24)
B25	=ЕСЛИ(E24<F24; D24; B24)
C25	=(A25+B25)/2-0,0001/3
D25	=(A25+B25)/2+0,0001/3
E25	=2*C25^2+EXP(-C25)
F25	=2*D25^2+EXP(-D25)
G25	=B25-A25

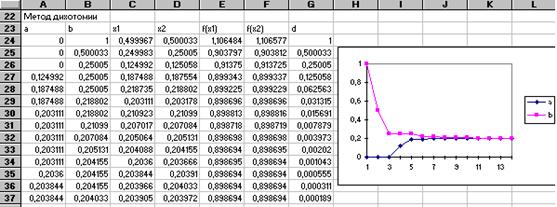
Из вычислений видно, что достаточно 12 итераций для получения решения с заданной точностью. Для построения диаграммы, иллюстрирующей изменения концов интервала неопределенности, следует выделить блок А23:В37 и воспользоваться Мастером Диаграмм, выбрав тип График и формат 1.

4.2. Метод золотого сечения.

Как известно, золотым сечением отрезка называют деление отрезка так, что отношение длины всего отрезка к длине большей части равно отношению длины большей части к меньшей части отрезка. Нетрудно проверить, что золотое сечение отрезка [a,b] производят две симметричные точки

Х₁ = a + L(b-a) и X₂ = b - L(b-a), где L = (3 - Ö(5))/2.

Заметим, что точка Х₁ в свою очередь производит золотое сечение отрезка
[a, X₂], а точка X₂ - золотое сечение отрезка [Х₁,b].

Опишем алгоритм поиска. Начальный отрезок [a,b] делим точками Х₁ и X₂ по правилу золотого сечения. Вычисляем значения функций f(Х₁) и f(X₂). Сравнение этих значений позволяет отбросить либо интервал [a,Х₁], либо интервал [X₂,b]. На оставшемся интервале уже есть одна точка, производящая его золотое сечение. Поэтому следует вычислить значение второй такой точки. На этом заканчивается первая итерация. Таким образом на каждой итерации, начиная со второй, требуется лишь одно вычисление функции и при этом интервал неопределенности уменьшается на величину L ~ 0,382. Итерации продолжаются до тех пор, пока интервал неопределенности [a,b] не станет меньше заданной точности решения Е.

Пример 4.2.

Решим задачу примера 4.1 методом золотого сечения на том же рабочем листе, на котором приведено решение методом дихотомии. Величину L вычислим в ячейке Е39, а под решение отведем блок А41: G60. Приведем таблицу формул в соответствующих ячейках для первых двух итераций в строках 41 и 42. Формулы для остальных строк блока копируются из 42 строки. Для вычисления квадратного корня из 5 используется функция КОРЕНЬ Мастера Функций. В формулах строк 41 и 42 использован абсолютный адрес ячейки Е39, т.к. он не должен меняться при копировании.

Адрес	Формула
E39	(3-КОРЕНЬ(5))/2
A41
B41
C41	=A41+(B41-A41)*$E$39
D41	=B41-(B41-A41)*$E$39
E41	=2*C41^2+EXP(-C41)

F41	=2*D41^2+EXP(-D41)
G41	=B41-A41
A42	=ЕСЛИ(E41>F41; C41; A41)
B42	=ЕСЛИ(E41<F41; D41; B41)
C42	=ЕСЛИ(E41>F41; D41; A42+(B42-A42)*$E$39
D42	=ЕСЛИ(E41<F41; C41; B42-(B42-A42)*$E$39)
E42	=2*C42^2+EXP(-C42)
F42	=2*D42^2+EXP(-D42)
G42	=B41-A41

Как видно из таблицы, и в этом случае широко используется функция ЕСЛИ Мастера функций. После того как блок будет заполнен формулами, EXCEL предоставит решение задачи. Данный метод сходится медленнее метода дихотомии и количество итераций для получения решения с одинаковой точностью методом золотого сечения будет большей. Как и в предыдущем примере, можно построить диаграмму изменения концов интервала неопределенности.

4.3. Встроенная подпрограмма EXCEL “ Поиск решения ”.

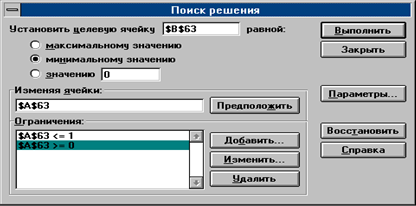
EXCEL имеет специальную подпрограмму, позволяющую решать многие оптимизационные задачи, в том числе и задачи одномерной оптимизации. Продемонстрируем применение этой подпрограммы для решения задачи из примера 4.1. Будем искать решение на том же рабочем листе. Выделим ячейку А63 для значений независимой переменной Х, а ячейку В63 - для значений целевой функции f(X). Занесем в ячейку В63 формулу =2*А63^2 + EXP(-A63).

Теперь можно запустить подпрограмму, дав команду меню Сервис- Поиск решения. Откроется диалог Поиск решения. В поле Установить целевую ячейку занесем адрес В63, с помощью переключателей в левой части диалога установим режим поиска минимального значения в этой ячейки. В поле Изменяя ячейки занесем адрес А63 и, наконец, в списке Ограничения укажем дополнительные условия нахождения минимума c помощью кнопки Добавить. Для нашей задачи таких условий два: А63³0 и A63£1. Они указывают начальный интервал неопределенности, на котором целевая функция унимодальна.

Поиск решения начинается щелчком на кнопке Выполнить. Когда программа находит решение, открывается новый диалог Результаты поиска решений. Щелчком на кнопке ОК можно сохранить найденное решение.

5. МНОГОМЕРНЫЕ ЗАДАЧИ ОПТИМИЗАЦИИ.

В этом разделе будут рассмотрены методы, позволяющие находить минимум целевой функции многих переменных u = f(X₁,X₂,..., Xn). Из курса математического анализа известно, что значения независимых переменных, при которых целевая функция достигает минимума, можно найти, решая систему нелинейных уравнений

du/dX₁ = 0,

du/dX₂ = 0,

....................

du/dXn = 0.

Рассмотренный прием можно использовать лишь для дифференцируемой целевой функции, но и в этом случае могут возникнуть серьезные вычислительные трудности (см. раздел 3).

Здесь мы рассмотрим численные методы оптимизации, основанные на идее целенаправленного поиска минимума. Эти методы различаются прежде всего по характеру изменения целевой функции: если нет никаких ограничений ни на изменение независимых переменных, ни на значения целевой функции, то это - методы безусловной оптимизации. При наличии каких-либо ограничений используются методы условной оптимизации.

Кроме того, методы многомерной оптимизации классифицируются по возможности использования частных производных от целевой функции: если производные не используются, то это - методы прямого поиска, в противном случае - градиентные методы.

5.1. Безусловная оптимизация: метод покоординатного спуска.

Это метод прямого поиска, в котором используются только значения целевой функции. Чтобы воспользоваться этим методом, необходимо иметь следующие исходные данные:

а) формулу целевой функции f(X₁,X₂,..., Xn),

б) Е - точность нахождения значений независимых переменных, при которых функция достигает минимума,

в) начальные приближения X₁₀,X₂₀..., Xn₀.

Зафиксируем все значения Х-ов в виде начальных приближений, кроме первого. Тогда f(X₁, X₂₀..., Xn₀) - функция одной переменной X₁. Решая задачу одномерной оптимизации, найдем минимум этой функции по координате X₁ при фиксированных остальных координатах - X₁₁. В этом состоит первый шаг процесса оптимизации, заключающийся в спуске по координате X₁.

Зафиксируем теперь все координаты, кроме X₂. Снова решая одномерную задачу оптимизации, находим минимум функции по координате X₂. Далее процедура повторяется до Xn. На этом заканчивается первая итерация.

Таким образом, метод покоординатного спуска сводит многомерную задачу оптимизации к многократному решению одномерных задач по каждой независимой пременной.

После каждой итерации вычисляется

D = çХ_1i+1 - X_1iç + çХ_2i+1 - X_2iç +.... +çХn_i+1 - Xn_iç

и если D<=E, то вычисления прекращаются и последний набор Х-ов считается решением. В противном случае проводится следующая итерация.

Пример 5.1.

Число независимых переменных равняется двум. Ограничения отсутствуют. Требуется найти минимум функции

u = (X₂-X₁²)² + (1-X₁)²

из начальной точки (0,5;0,5) c точностью 0,0001. Проанализировав функцию, заметим, что она будет иметь минимум, равный нулю. Для чего и первое, и второе слагаемое тоже должны быть равны нулю. Откуда координаты точки минимума (1;1).

Решим эту задачу на EXCEL. Откроем новый рабочий лист. Выделим столбец А под значения X₁, столбец В - под значения X₂, в столбец С будем заносить значения целевой функции и, наконец, в столбец D - значения погрешности D.

Занесем в ячейки А3 и В3 значения начальных приближений, равных 0,5 и в ячейку С3 формулу =(В3-А3^2)^2+(1-A3)^2. Скопируем эту формулу в блок ячеек С4:С17. На этом заканчивается подготовительный этап.

1 итерация.

1 шаг. Скопируем содержимое ячейки В3 в ячейку В4. Сделаем текущей ячейку С4. Процесс одномерной оптимизации для нахождения X₁ выполним с помощью подпрограммы EXCEL Поиск решения. Вызовем эту подпрограмму командой меню Сервис- Поиск решения. В открывшемся диалоге в поле Установить целевую ячейку занесем адрес С4, а в поле Изменяя ячейки - адрес А4. Щелкнем по кнопке Выполнить и, во вновь открывшемся диалоге Результаты поиска решения щелкнем по кнопке ОК. В результате в ячейке А4 получим числовое значение, при котором целевая функция достигает минимального значения в ячейке С4 по координате X₁.

2 шаг. Скопируем содержимое ячейки А4 в ячейку А5. Сделаем текущей ячейку С5. Дадим команду меню Сервис- Поиск решения. В открывшемся диалоге в поле Установить целевую ячейку занесем адрес С5, а в поле Изменяя ячейки - адрес В5. Щелкнем по кнопке Выполнить и, во вновь открывшемся диалоге Результаты поиска решения щелкнем по кнопке ОК. В результате в ячейке В5 получим числовое значение, при котором целевая функция достигает минимального значения в ячейке С5 по координате X₂.

3 шаг. Занесем в ячейку D5 формулу =ABS(A3-A5)+ABS(B3-B5) для вычисления погрешности решения на первом шаге. На этом заканчивается первая итерация.

Вторая и все последующие итерации проводятся аналогично, но с учетом соответствующих адресов ячеек. Например, во второй итерации будут участвовать адреса ячеек в 6 и 7 строках. Результаты проведения первых семи итераций представлены в таблице. Как видно, значения целевой функции уменьшаются от шага к шагу, но метод сходится чрезвычайно медленно.

Можно построить диаграмму изменения на каждой итерации, выделив блок А2:В17 с помощью Мастера Диаграмм, выбрав тип диаграммы XY-точечная и формат 2. На диаграмме хорошо видны перпендикулярные ломаные линии движения от точки к точке параллельно одной из осей координат.

5.2. Безусловная оптимизация: метод наискорейшего спуска.

Это метод градиентного поиска, в котором используются как значения целевой функции, так и значения ее первых частных производных. Чтобы воспользоваться этим методом, необходимо иметь следующие исходные данные:

а) формулу целевой функции f(X₁,X₂,..., Xn),

б) Е - точность нахождения значений независимых переменных, при которых функция достигает минимума,

в) начальные приближения X₁₀,X₂₀..., Xn₀,

г) формулы первых частных производных целевой функции по каждой независимой переменной.

С помощью рассмотренного ранее метода покоординатного спуска осуществляется поиск в направлении, параллельном одной из осей координат, до точки минимума в этом направлении. Кажется разумным попытаться модифицировать этот метод таким образом, чтобы на каждом шаге поиск минимума производился вдоль “наилучшего” направления. Не ясно, какое направление является наилучшим, но известно, что направление градиента является направлением наискорейшего возрастания функции. Следовательно, противоположное направление - антиградиента - является направлением наискорейшего убывания функции.

Множество точек, для которых целевая функция имеет постоянное значение, называется линией уровня. Направление градиента перпендикулярно к любой точке линии уровня. Под градиентом понимается вектор-столбец из первых частных производных целевой функции, если она непрерывна и дифференцируема.

Идея метода наискорейшего спуска состоит в следующем. Выбираем начальную точку и вычисляем в ней градиент целевой функции. Определяем направление поиска, противоположное градиенту. Решая задачу одномерной оптимизации, ищем точку минимума целевой функции по этому направлению.

Например, для функции двух переменных формулы первой итерации будут иметь вид

u = f(X_1нов,X_2нов) Þ min,

где X_1нов = X₁₀- h(du/dX₁)_X10 и X_2нов = X₂₀ -h(du/dX₂) _X20, а h - длина отрезка от точки нулевого приближения до точки минимума по выбранному направлению. Эта длина определяется методом одномерной оптимизации. На этом кончается первая итерация.

В найденной точке (X_1нов,X_2нов) снова вычисляем градиент, снова определяем направление поиска, снова методом одномерной оптимизации ищем точку минимума. Эти итерации продолжаются до тех пор, пока не выполнится условие прекращения вычислений, а именно: квадратный корень из суммы квадратов частных производных целевой функции должен быть меньше заданной точности Е.

Пример 5.2.

Решим задачу примера 5.1 методом наискорейшего спуска. Для этого прежде всего найдем частные производные целевой функции

u = (X₂-X₁²)² + (1-X₁)²,

du/dX₁ = - 4(X₂-X₁²) X₁-2(1-X₁),

du/dX₂ = 2(X₂-X₁²).

Составляющие антиградиента должны быть взяты с обратным знаком

antigrad u = {- du/dX₁, -du/d X₂ }.

Будем решать задачу на том же рабочем листе, где мы исследовали метод покоординатного спуска. Выделим столбец А под переменную h, столбцы В и С - под X₁,X₂, столбцы D и Е - под составляющие антиградиента, столбцы F и G - под X_1нов,X_2нов, столбец Н - под целевую функцию u, столбец I - под переменную D. Приведем таблицу формул в соответствующих ячейках для первых двух итераций в строках 21 и 22. Заметим, что числовые значения в столбце А появляются в результате выполнения подпрограммы EXCEL Поиск решения для решения задачи одномерной оптимизации. Формулы блока В23:I28 получаются путем копирования в них формул блока В22:I22.

ячейка	формула
B21	0,5
C21	0,5
D21	=4*(C21-B21^2)*B21+2*(1-B21)
E21	=-2*(C21-B21^2)
F21	=B21+A21*D21
G21	=C21+A21*E21
H21	=(G21-F21^2)^2+(1-F21)^2
I21	=КОРЕНЬ(D21^2+E21^2)
B22	=F21
C22	=G21
D22	=4*(C22-B22^2)*B22+2*(1-B22)
E22	=-2*(C22-B22^2)
F22	=B22+A22*D22
G22	=C22+A22*E22
H22	=(G22-F22^2)^2+(1-F22)^2

После подготовки формул в блоке А21:I28, проведем первую итерацию. Для этого сделаем текущей ячейку Н21. Дадим команду меню Сервис- Поиск решения. В появившемся диалоге занесем в поле Установить целевую ячейку адрес Н21, а в поле Изменяя ячейки - адрес А21. Щелкнув по кнопке Выполнить, получим новый диалог, в котором щелкнем по кнопке ОК. В результате в ячейке А21 получим значение h, а ячейках F21 и В22 - новое значение Х1, в ячейках G21 и С22 - новое значение Х2.

Теперь можно приступить ко второй итерации, сделав текущей ячейку Н22. Снова используя подпрограмму Поиск решения так же, как и в первой итерации, получим очередные новые значения шага и независимых переменных. Продолжая итерации, как видно из таблицы, можно получить решение с заданной точностью за семь итераций. Точность решения контролируется по столбцу I.

Выделяя блок В20:С28, можно построить диаграмму, аналогично примеру 5.1. На ней изображены перпендикулярные ломаные линии, причем в отличие от примера 5.1 их направление не совпадает с направлениями координатных осей.

5.3. Безусловная оптимизация: подпрограмма EXCEL “Поиск решения”.

Подпрограмма Поиск решения позволяет решать не только задачи одномерной, но и многомерной оптимизации. В ней можно воспользоваться двумя более мощными методами: методом сопряженных градиентов и методом Ньютона. Оба метода - градиентные. Отличие их от метода наискорейшего спуска заключается в том, что составляющие антиградиента в них - частные производные целевой функции- вычисляются не аналитически, а методами численного дифференцирования.

Продемонстрируем применение этой подпрограммы для решения задачи примера 5.1 на том же рабочем листе. Выделим ячейки А31 и В31 под независимые переменные Х₁ и Х₂, а ячейку С31 - под целевую функцию u.

Занесем в ячейку С31 формулу =(В31- A31^2)^2+(1-A31)^2. Cделав ячейку С31 текущей, вызовем подпрограмму командой меню Сервис- Поиск решения. В появившемся диалоге занесем в поле Установить целевую ячейку адрес С31, а в поле Изменяя ячейки - адреса A31:B31.

Теперь надо щелкнуть по кнопке Параметры. Откроется диалог Параметры поиска решения, в котором можно выбрать переключатели поля Оценка - квадратичная, поля Производные - прямые, поля Метод - сопряженных градиентов.

Щелкнув по кнопке Выполнить, получим новый диалог, в котором щелкнем по кнопке ОК. В результате в ячейке А31 получим минимальное значение Х₁, а в ячейке В31 - минимальное значение Х₂. Легко убедиться, что оба они очень близки к 1.

При желании можно повторить вычисления, выбрав другие значения переключателей и сравнив результаты вычислений.

5.4. Условная оптимизация: метод штрафных функций.

Чтобы воспользоваться этим методом, необходимо иметь следующие исходные данные:

а) формулу целевой функции f(X₁,X₂,..., Xn),

б) Е - точность нахождения значений независимых переменных, при которых функция достигает минимума,

в) начальные приближения X₁₀,X₂₀..., Xn₀,

г) формулы функций - ограничений в виде равенств g(X₁,X₂,..., Xn)=0,

д) формулы функций - ограничений типа неравенств h(X₁,X₂,..., Xn)>=0.

Здесь важно, что ограничения записаны в канонической форме, т.е. они или равны, или больше или равны нулю.

Сущность метода состоит в том, что задачу условной оптимизации при наличии ограничений мы заменяем на задачу безусловной оптимизации: поиска минимума некоторой другой - расширенной целевой функции без каких-либо ограничений

R(X₁,X₂,..., Xn)= f (X₁,X₂,..., Xn)+ Bs(X₁,X₂,..., Xn),

где s - штрафная функция, В - коэффициент штрафа.

Штрафная функция должна учитывать заданные ограничения, а именно:

1) она должна равняться нулю для всех значений Х-ов, удовлетворяющих заданным ограничениям, т.е. когда все Х лежат в разрешенной области,

2) она должна быть очень большой, стремиться к бесконечности для тех точек, которые лежат в запрещенной области там, где ограничения не выполняются.

Таким образом, при выполнении ограничений в разрешенной области функции f (X₁,X₂,..., Xn) и R(X₁,X₂,..., Xn) имеют один и тот же минимум. Если хотя бы одно из ограничений нарушится, значение штрафной функции сильно возрастает и значение функции R(X₁,X₂,..., Xn) значительно удаляется от минимума функции f(X₁,X₂,..., Xn). Другими словами, при несоблюдении ограничений на целевую функцию налагается “штраф”.

Пусть есть только по одному ограничению типа равенства и неравенства. Тогда шрафную функцию можно записать в виде

s(X₁,X₂,..., Xn)= g²(X₁,X₂,..., Xn)+ h²(X₁,X₂,..., Xn) {1 - sign[h(X₁,X₂,..., Xn)]},

где sign[Z] -знаковая функция, равная 1 при Z>0 и равная -1 при Z<0.

Если ограничение типа равенства выполняется, то g = 0, в противном случае первое слагаемое штрафной функции g²(X₁,X₂,..., Xn) больше нуля и при умножении на коэффициент штрафа сильно увеличивает значение расширенной целевой функции.

Если ограничение типа неравенства выполняется, то h(X₁,X₂,..., Xn) больше нуля, т.е. знаковая функция равна 1 и выражение в фигурных скобках равно нулю. В противном случае это выражение равно2, а значит второе слагаемое штрафной функции больше нуля и при умножении на коэффициент штрафа сильно увеличивает значение расширенной целевой функции. Таким образом, эта формула обеспечивает выполнение условий, наложенных на штрафную функцию. Если ограничений любого вида несколько, то для каждого из низ записываются аналогичные формулы и все они суммируются.

Дата добавления: 2014-12-27