В примерах на EXCEL 5 страница

Отведем строку 20 для вычисления интегралов. Занесем в ячейку В20 формулу =СУММ(В3:В18)*0,05, где СУММ - встроенная функция EXCEL, вызываемая Мастером Функций. В ячейку С20 введем формулу =СУММ(С3:С17)*0,1. Числа, появившиеся в этих ячейках, достаточно сильно различаются между собой.

Проведем аналогичные операции в столбцах D и Е для вычисления интеграла методом прямоугольников с узлом справа. Следует обратить внимание на то, что на этот раз в формулах отсутствуют значения, равные Х₀.

В столбцах F и G проведем вычисления интеграла методом трапеций. Здесь следует обратить внимание на формулы в строках 3 и 19. В них подынтегральная функция должна быть поделена на 2 согласно формуле трапеций.

Для метода прямоугольников с узлом в центре выделим столбцы Н и I. В ячейку Н3 должна быть введена формула =1/(1+A3+0,025), а в ячейку I3 - формула =1/(1+A3+0,5). Далее эти формулы должны быть скопированы до строки 18.

И, наконец, для метода парабол возьмем столбцы J и K. В столбце J вычислим интеграл с шагом 0,05. Введем в ячейку J3 формулу =1/(1+A3), в ячейку J4 - формулу =4/(1+A4), в ячейку J5 - формулу =2/(1+A5). Далее выделим блок J4:J5 и скопируем его в блок J6:J18. Затем в ячейку J19 запишем формулу =1/(1+A19). При вычислении суммы в ячейке J20 надо не забыть, что в формуле участвует выражение h/3, а не просто h.

Что касается столбца К, то формула в ячейке К3 совпадает с ячейкой J3, в ячейке К5 подынтегральная функция должна быть умножена на 4, а в ячейке К7 - умножена на 2 и т.д., кроме ячейки К19.

Как видно из таблицы, метод парабол обладает наибольшей точностью из всех рассмотренных методов.

8. ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ

Как известно, лишь небольшое число типов уравнений первого порядка допускает интегрирование в квадратурах. Еще реже удается получить решение в элементарных функциях. Тем большее значение имеют численные методы, позволяющие получить приближенное решение одного обыкновенного дифференциального уравнения первого порядка.

Пусть требуется найти приближенное решение уравнения

dY/dX = Y’ = f(X,Y),

удовлетворяющее начальному условию Y(X₀) = Y₀. Численное решение задачи состоит в вычислении таблицы приближенных значений Y₁,Y₂,..., Y_n решения уравнения Y(X) в точках Х₁,Х₂,....,Х_n. Обычно, X_i = X₀+ih, где i=1,2,...,n. Точки Х_i называются узлами сетки, а величина h - шагом, причем 0<h<1.

8.1. Метод Эйлера.

Этот метод относится к группе одношаговых методов, в которых для расчета точки Y_i+1 = Y(X_i+1) требуется информация только о последней вычисленной точке Y_i. Формула Эйлера вычисления любого Y такова

Y_i+1 = Y_i +hf(X_i,Y_i), где i=0,1,2,...,n-1.

Для оценки погрешности применяется правило двойного пересчета: расчет повторяют с шагом h/2 и погрешность более точного значения Yi* при шаге h/2 оценивают так

max çY_i * - Y_i ç<E для i=1,2,...,n.

Метод Эйлера называют методом первого порядка, поскольку его погрешность пропорциональна h и для вычисления новой точки решения функция f вычисляется лишь один раз.

Метод Эйлера можно усовершенствовать множеством различных способов. Из этих способов наиболее распространены два. Это так называемые исправленный и модифицированный методы Эйлера.

Обозначим К₁ = f(X_i,Y_i). Тогда оба метода описываются формулой

Y_i+1 = Y_i +hФ(X_i,Y_i), где

Ф(X_i,Y_i) = a₁K₁ + a₂f(X_i+b₁h, Y_i+b₂hK₁).

Для исправленного метода a₁= a₂=0,5 и b₁= b₂=1.

Для модифицированного метода a₁=0, a₂=1 и b₁= b₂=0,5.

Это методы второго порядка, погрешность решения пропорциональна h².

Пример 8.1.

Найти решение уравнения

Y’ = 0,25Y² + X²

c начальным условием Y(0) = -1 на отрезке [0;0,5] с шагом 0,1. Точность решения принять Е=0,0001.

Откроем новый рабочий лист EXCEL. Отведем столбец А под значения Х. Учитывая правило двойного пересчета занесем в блок А3:А13 значения Х от 0 до 0,5 с шагом 0,05. Значения Y по методу Эйлера с шагом 0,05 и 0,1 будем вычислять в столбцах B и C, для оценки погрешности отведем столбец D. Проведем для сравнения здесь же решение этой задачи исправленным методом Эйлера. Столбцы E и F отведем под значения Y_исп с шагом h и h/2, столбцы G и H - под значения коэффициента K₁, столбцы I и J - под значения функции Ф_исп, столбец К - для оценки погрешности. В ячейки В3, С3, E3 и F3 внесем начальные значения Y=-1. Основные формулы в строках 3, 4 и 5 приведены в таблице

ячейка	формула
Строка 3
B3	-1
C3	-1
D3	=ABS(C3-B3)
E3	-1
F3	-1
G3	=0,25*E3^2+A3^2
H3	=0,25*F3^2+A3^2
I3	=0,5*G3+0,5*(0,25*(E3+0,05*G3)^2+(A3+0,05)^2)
J3	=0,5*H3+0,5*(0,25*(F3+0,1*H3)^2+(A3+0,1)^2)
K3	=ABS(F3-E3)
Строка 4
B4	=B3+0,05*(0,25*B3^2+A3^2)
E4	=E3+0,05*I3
Строка 5
C5	=C3+0,1*(0,25*C3^2+A3^2)
F5	=F3+0,1*J3

Формулы в остальных строках получаются копированием содержимого строк, указанных в таблице. Результаты вычислений EXCEL приведены ниже. Как видно из таблицы, расчеты методом Эйлера на порядок хуже, чем расчеты исправленным методом.

8.2. Метод Рунге-Кутта четвертого порядка.

По этому одношаговому методу вычисления проводятся по формуле

Y_i+1 = Y_i +hФ(X_i,Y_i), где

Ф(X_i,Y_i) = (K₁+2K₂+2K₃+K₄)/6

и К₁ = f(X_i,Y_i),

K₂=f(X_i+h/2,Y_i+hК₁/2),

K₃=f(X_i+h/2,Y_i+hК₂/2),

K₄=f(X_i+h,Y_i+hК₃).

Метод Рунге-Кутта имеет порядок точности h⁴ на всем отрезке интегрирования. Оценка погрешности метода очень затруднительна. Для оценки погрешности применяется правило двойного пересчета: расчет повторяют с шагом h/2 и погрешность более точного значения Yi* при шаге h/2 оценивают так

max {çY_i * - Y_i ç/15}<E для i=1,2,...,n.

Пример 8.2.

Решим задачу примера 8.1 методом Рунге-Кутта на том же рабочем листе. Отведем блок ячеек А17:А22 под значения Х с шагом 0,1. Соответственно, в столбце В будем вычислять Y, в столбцах С,D,E,F - значения коэффициентов К₁, K₂, K₃ и K₄. Столбец G отведем под Ф(X_i,Y_i). Основные формулы в строках 17 и 18 приведены в таблице.

ячейка	формула
С17	=0,25*B17^2+A17^2
D17	=0,25*(B17+0,05*C17)^2+(A17+0,05)^2
E17	=0,25*(B17+0,05*D17)^2+(A17+0,05)^2
F17	=0,25*(B17+0,1*E17)^2+(A17+0,1)^2
G17	=C17+2*D17+2*E17+F17
B18	=B17+0,1*G17/6

Содержимое остальных ячеек в строках с 18 по 22 получается копированием из строк 17 и 18.Результаты решения приведены ниже. Для оценки погрешности следует провести те же вычисления с шагом, равным 0,05.

8.3. Метод прогноза и коррекции: метод Адамса.

В методах прогноза и коррекции каждое новое значение Yi определяют в два этапа. На первом определяют приближенное значение, которое называют прогнозом. Затем на втором этапе его уточняют с помощью итерационного процесса коррекции. Этот итерационный процесс продолжают до тех пор, пока не будет достигнута заданная точность решения. Таким образом, одно из достоинств метода прогноза и коррекции состоит в том, что одновременно с решением контролируется оценка погрешности.

С другой стороны, этот метод не является одношаговым, т.е. для вычисления прогноза необходимо иметь уже несколько вычисленных точек решения.

Пусть для уравнения

dY/dX = Y’ = f(X,Y),

с начальным условием Y(X₀) = Y₀ найдены каким-либо способом (методом Эйлера, Рунге-Кутта и т.п.) три последовательных значения искомой функции, так называемый начальный отрезок: Y₁, Y₂ и Y₃ для точек Х₁,Х₂ и Х₃, вычисленных с шагом h. Имея эти значения можно вычислить значения функции f₁=f(Х₁,Y₁),f₂₌f(Х₂,Y₂), f₃₌f(Х₃,Y₃) и f₀ =f(X₀,Y₀).

Метод Адамса состоит в вычислении Y₄ сначала по формуле прогноза

Y_4pred = Y₃+hФ_pred/24 = Y₃+h(55f₃-59f₂+37f₁-9f₀)/24

а затем уточнения этого значения, вычислив f_4pred=f(Х₄,Y_4pred) и применив формулу коррекции

Y_4kor= Y₃+hФ_kor/24 =Y₃+h(9f_4pred+19f₃-5f₂+ f₁)/24.

Эти формулы имеют достаточно большую точность и дают погрешность порядка h⁴. Обычно вычисляют D=çY_4kor - Y_4predç и если D<E, то переходят к вычислению следующей точки по тем же самым формулам, вводя переобозначения. Если же D>E, то проводят одну или несколько итераций по формуле коррекции, вычисляя f_4pred=f(Х₄,Y_4pred) и подставляя в эту формулу Y_4kor вместо Y_4pred. Как правило, для достижения заданной точности хватает одной или двух итераций.

Пример 8.3.

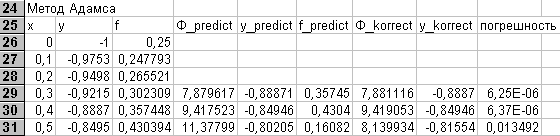
Решим методом Адамса задачу примера 8.1. Из примера 8.2 возьмем вычисленные значения Y₁, Y₂ и Y₃. Продолжим вычисления по формулам Адамса для Х₄ и Х₅ на том же рабочем листе. Отведем блок А26:А31 под значения Х с шагом 0,1. В блок В26:В29 занесем значения Y из примера 9.2. В столбце С будем вычислять значения функции f на каждом шаге. В остальных столбцах будем последовательно располагать значения Ф_pred, Y_4pred, f_4pred, Ф_kor, Y_4kor, D. Необходимые для вычислений формулы приведены в таблице

ячейка	формула
C26	=0,25*B26^2+A26^2
D29	=55*C29-59*C28+37*C27-9*C26
E29	=B29+0,1/24*D29
F29	=0,25*E29^2+A30^2
G29	=9*F29+19*C29-5*C28+C27
H29	=B29+0,1/24*G29
I29	=ABS(E29-H29)
B30	=H29

Формулы в остальных ячейках, участвующих в вычислениях, получаются копированием. Результаты вычислений приведены в таблице

Видно, что погрешность удовлетворяет заданному значению для последних двух точек и итераций не требуется. В противном случае следовало бы воспользоваться встроенной подпрограммой EXCEL Поиск решения так, как это описано в разделе 6.

9. РЕШЕНИЕ СИСТЕМ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ.

Рассмотренные в предыдущем разделе одношаговые методы могут быть использованы для решения систем обыкновенных дифференциальных уравнений или для нахождения решения одного дифференциального уравнения высокого порядка. В последнем случае введением новых переменных оно сводится к решению системы дифференциальных уравнений первого порядка. Рассмотрим последовательно решение задачи Коши и краевой задачи применительно к системам таких уравнений.

9.1. Задача Коши.

Для получения однозначного решения системы дифференциальных уравнений должны быть заданы дополнительные условия. Их должно быть задано столько, каков порядок решаемой системы. Если все эти условия задаются в одной точке, т.е. при одном значении Х=Х₀, то такая задача называется задачей Коши. Эти дополнительные условия называются начальными условиями, а Х₀ - называется начальной точкой.

Покажем применение метода Рунге-Кутта четвертого порядка для решения задачи Коши системы двух уравнений вида

dY/dX = f₁(X,Y,Z)

dZ/dX = f₂(X,Y,Z).

Начальные условия зададим в виде Y(Х₀)=Y₀ и Z(Х₀)=Z₀.

По аналогии с разделом 8.2 запишем формулы Рунге-Кутта для приближенного решения этой системы

Y_i+1=Y_i+hФ₁= (K₁+2K₂+2K₃+K₄)/6,

Z_i+1 = Z_i+hФ₂=(L₁+2L₂+2L₃+L₄)/6,

где

K₁= f₁(X_i,Y_i,Z_i) и L₁= f₂(X_i,Y_i,Z_i),

K₂= f₁(X_i +h/2, Y_i+hK₁/2, Z_i+hL₁/2) и L₂= f₂(X_i +h/2, Y_i+hK₁/2, Z_i+hL₁/2),

K₃= f₁(X_i +h/2, Y_i+hK₂/2, Z_i+hL₂/2) и L₃= f₂(X_i +h/2, Y_i+hK₂/2, Z_i+hL₂/2),

K₄= f₁(X_i +h,Y_i+hK₃, Z_i+hL₃) и L₄= f₂(X_i +h,Y_i+hK₃, Z_i+hL₃).

В этих формулах i = 0,1,2,...,n-1. Для оценки погрешности используется правило двойного пересчета точно так же, как и при решении одного уравнения.

К решению подобной системы уравнений можно свести решение задачи Коши для уравнения второго порядка

d²Y/dX² = f(X,Y,dY/dX)

с начальными условиями Y(Х₀)=Y₀ и Y’(Х₀)=Z₀.

Введем новую переменную Z(X) = dY/dX. Тогда исследуемое уравнение заменяется следующей системой из двух уравнений

dZ/dX= f(X,Y,Z)

dY/dX=Z,

с начальными условиями Y(Х₀)=Y₀ и Z(Х₀)=Z₀.

Пример 9.1.

Применяя метод Рунге-Кутта, вычислить на отрезке [1;1,5] таблицу значений решения уравнения

Y” +Y’/X+Y=0

с начальными условиями Y(1)=0,77 и Y’(1)=-0,5, выбрав шаг 0,1 с погрешностью 0,0001.

С помощью подстановки новой переменной Z, перейдем к решению системы уравнений

Y’=Z

Z’=-Z/X-Y,

с начальными условиями Y(1)=0,77 и Z(1)=-0,5.

Откроем новый рабочий лист EXCEL и выделим в нем столбцы А, В и С под переменные X, Y и Z. В последующие столбцы будем вычислять последовательно, как и в примере 8.2, значения коэффициентов K_i, Ф₁, L_i, Ф₂. Пусть значения Х помещаются в блок А3:А8. Тогда в ячейки В3 и С3 занесем начальные значения Y(1) и Z(1). Формулы в остальных ячейках строки 3 и 4 приведены в таблице

Формулы в остальных строках решения получаются путем копирования.

Результаты решения задачи с шагом 0,1 приведены в таблице. Для оценки погрешности полученного решения следует провести решение вновь с шагом, равным половине начального, т.е. 0,05.

9.2. Краевая задача: метод стрельбы.

Если при решении дифференциального уравнения высокого порядка дополнительные условия, определяющие однозначное решение, заданы при разных значениях независимой переменной, обычно в двух точках, являющихся границами области решения уравнения, то такая задача называется краевой. При этом сами дополнительные условия называются граничными или краевыми.

Рассмотрим решение краевой задачи для уравнения второго порядка

d²Y/dX² = f(X,Y,dY/dX)

с граничными условиями Y(Х₀)=Y₀ и Y(Х_n)=Y_n.

Сущность метода стрельбы заключается в сведении краевой задачи к многократному решению задачи Коши для того же уравнения с подбором недостающего начального условия Y’(Х₀)=Z₀ так, чтобы решение задачи Коши в точке Х_n совпадало бы с заданным граничным условием Y_n с заданной точностью Е.

Алгоритм метода стрельбы таков.

1) выбирается любое значение Z₀,

2) исходное уравнение второго порядка приводится к системе из двух уравнений первого порядка введением дополнительных переменных,

3) полученная система решается численным методом, например, методом Рунге-Кутта при некотором начальном значении шага h и запоминается полученное решение в точке Х_n,

4) шаг h уменьшается в два раза и вновь находится решение в точке Х_n,

5) если новое решение отличается от старого меньше, чем на заданную точность Е, то переходят к следующему этапу; иначе - возвращаются к предыдущему этапу и снова уменьшают шаг h в два раза и т.д. до тех пор, пока не будет достигнута заданная точность,

6) при выбранном значении шага, обеспечивающего необходимую точность решения, многократно решают задачу Коши, подбирая начальное условие Y’(Х₀)=Z₀ так, чтобы получаемое в точке Y(Х_n) решение отличалось от заданного краевого условия Y_n меньше, чем на заданную величину Е.

Пример 9.2.

Решим задачу примера 10.1 с граничными условиями Y(1)=0,77 и Y(1,5)=0,49281, выбрав шаг 0,1 с погрешностью 0,001.

Для этого можно использовать таблицу примера 10.1, где был запрограммирован метод Рунге-Кутта. Изменяя значение в ячейке С3, нужно добиться получения в ячейке В8 заданного граничного значения. Конечно, сначала по правилу двойного пересчета следует убедиться в том, что выбранное значение шага h достаточно для достижения необходимой точности решения.

9.3. Краевая задача: метод прогонки.

Рассмотрим метод прогонки на примере решения уравнения второго порядка вида

Y”+p(X)Y’+q(X)Y=f(X)

на отрезке [Х₀, Х_n] с заданными граничными условиями Y(Х₀)=Y₀=А и Y(Х_n)=Y_n=В. Смысл решения заключается в расчете таблицы приближенных значений искомой функции Y(Х) в узлах Х_i= Х₀+ih, где h=(Х_n - Х₀)/n и i=1,2,...,n-1.

Заменим приближенно в каждом внутреннем узле производные Y” и Y’ конечными центрально-разностными отношениями

Y_i“=(Y_i+1 -2Y_i + Y_i-1)/h² и Y_i‘=(Y_i+1 - Y_i-1)/(2h).

Обозначим p_i=p(Х_i), q_i=q(Х_i), f_i=f(Х_i).

Используя эти формулы, приближенно заменим исходное дифференциальное уравнение второго порядка на систему линейных алгебраических уравнений

(Y_i+1 -2Y_i + Y_i-1)/h² + p_i (Y_i+1 - Y_i-1)/(2h) + q_iY_i = f_i,

где i=1,2,...,n-1, Y₀=А и Y_n=В. Решив эту систему, получим таблицу приближенных значений искомой функции. При большом n непосредственное решение такой системы, например, методом Гаусса становится громоздким. Учитывая специфический вид полученной системы алгебраических уравнений, а именно- что матрица коэффициентов ее трехдиагональна, применим специальный метод решения, называемый методом прогонки.

Запишем систему в виде

a_i Y_i-1+b_i Y_i +c_i Y_i+1 =d_i ,

где a_i =1-hp_i /2, b_i = h²q_i -2, c_i =1+hp_i /2, d_i = h²f_i.

Введем дополнительные переменные

v_i = - c_i /(b_i + a_i v_i-1) и u_i = (d_i - a_i u_i-1)/(b_i + a_i v_i-1).

Чтобы сделать схему вычислений однородной, положим a₀=0 и c_n=0. Тогда v_n=0 и Y_n=u_n. Кроме того, v₀ = - c₀/b₀ и u₀ = d₀/b₀.

Тогда решение системы определяется формулой

Y_i = u_i + v_i Y_i+1 .

Пример 9.3.

Решим задачу примера 9.1 с граничными условиями Y(1)=0,77 и Y(1,5)=0,49281, выбрав шаг 0,1 с погрешностью 0,001.

Как видно из условий задачи, h = 0,1, q=1, f=0, d=0, p=1/X для всех Х.

Откроем новый рабочий лист и выделим блок А4:А9 под значения Х от 1 до 1,5. В блок В5:В8 занесем значения 1/X, отведем столбцы С,D,E для текущих значений a_i, b_i, c_i, столбцы F и G - для значений v_i и u_i, а столбец Н - для значений Y.

Занесем числа: в ячейку F4 - ноль, в ячейки G4 и H4 - число 0,77. Соответственно, в ячейку F9 - тоже ноль, в ячейки G9 и H9 - число 0,49281.

Формулы ячеек в строке 5 представлены в таблице.

ячейка	формула
B5	=1/A5
C5	=1-B5*$B$2/2
D5	=$B$2^2-2
E5	=1+B5*$B$2/2
F5	=-E5/(D5+C5*F4)
G5	=-C5*G4/(D5+C5*F4)
H5	=G5+F5*H6

Формулы в строках 6,7,8 должны быть скопированы из строки 5. Результаты вычислений приведены ниже. Можно сравнить их с результатами расчетов в примере 10.2, чтобы оценить полученную погрешность.

10. ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

Метод сеток или метод конечных разностей является одним из самых распространенных в настоящее время методов численного решения уравнений с частными производными. В его основе лежит идея замены производных конечно-разностными отношениями. Мы ограничимся случаем двух независимых переменных.

Рассмотрим в качестве примера смешанную задачу для уравнения теплопроводности: найти значения функции U(X,T), удовлетворяющие уравнению

dU/dT = Dd²U/dX²

с начальными условиями (т.е. при Т=0) U(X,0) = f(X) и

краевыми условиями первого рода U(0,T) = g₁(T) и U(L,T) = g₂(T).

Таким образом может быть описана задача о распространении тепла в однородном стержне длины L, на концах которого поддерживается заданный температурный режим. Соответствующей заменой переменных эту задачу можно свести к каноническому уравнению при D=1 и L=1

dU/dT = d²U/dX²

Заметим, что начальные и граничные условия должны быть согласованы, т.е. U(0,0) = f(0)= g₁(0) и U(1,0)=f(1)= g₂(0).

Построим на плоскости X0T равномерную прямоугольную сетку с шагом h в направлении Х и шагом l - в направлении Т:

Х= ih (i= 0,1,2,...,n) и T=jk (j=0,1,2,...).

Обозначим Xi= ih и Tj= jk, а также U(Xi, Tj)=Ui,j. Любой узел этой сетки, номер которого (i,j), определяется координатами(Xi,Tj). Узлы сетки, лежащие на границе полуполосы Т>=0 и 0<=X<=1, называются граничными, все остальные узлы - внутренними. Начальные и краевые условия считаются заданными в граничных узлах сетки. Приближенно заменим в каждом внутреннем узле вторую частную производную по пространственной координате Х конечно-разностным отношением

(d²U/dX²)_i,j =(U_i,j-1 -2U_i,j + U_i,j+1)/h²,

а первую частную производную по временной координате - конечно-разностным отношением

(dU/dT)_i,j =(U_i,j+1 - U_i,j)/k.

Тогда вместо исходного дифференциального уравнения, получаем алгебраическое уравнение вида

(U_i,j+1 - U_i,j)/k = (U_i-1,j -2U_i,j + U_i+1,j)/h².

Обозначив q=k/h², приведем это уравнение к виду

U_i,j+1 =(1-2q)U_i,j + q(U_i-1,j+U_i+1,j).

Задавая i=0,1,2,..,n и j=0, увидим, что все слагаемые в правой части этого уравнения могут быть вычислены из граничных условий. Поэтому таким образом можно вычислить все значения U на первом временном слое при j=1. Далее, задавая j=1, можно вычислить по этой формуле значения функции U во всех узлах второго временного слоя при j=2 и т.д. Такая схема вычислений называется явной. Доказано, что вычисления по этой схеме будут устойчивы, если 0<q<= 0,5. Задавая q=0,5, получим алгебраическое уравнение

U_i,j+1 =(U_i-1,j+U_i+1,j)/2.

Таким образом, используя это уравнение, можно вычислить значения функции U на каждом временном слое через значения на предыдущем слое.

Пример 10.1.

Hайти значения функции U(X,T), удовлетворяющие уравнению

dU/dT = Dd²U/dX²

с начальными условиями (т.е. при Т=0) U(X,0) = Sin(pX) и 0<X<=1,

краевыми условиями первого рода U(0,T) = 0 и U(1,T) = 0.

Выберем по аргументу Х шаг h=0,1, т.е. n=10. Так как q=0,5, то по аргументу Т получаем шаг k=h²/2=0,005.

Откроем новый рабочий лист EXCEL. Отведем столбец А под номера временных слоев от 0 до, например, 25. Заполним блок А3:А28 числами от 0 до 25. Во второй строке в ячейки В2:L2 занесем значения пространственной координаты Х от 0 до 1. В блок В3:В28 и в блок L3:L28 занесем нули - значения краевых условий. В ячейку С3 занесем формулу =SIN(3,1415*C2) и скопируем ее в блок D3:K3. Тем самым введем в нулевой временной слой начальные условия. Далее в ячейку С4 введем основную расчетную формулу, полученную из алгебраического конечно-разностного уравнения =(B3+D3)/2. Эту формулу надо скопировать в блок С4:L28.

Результаты вычислений представлены в таблице для первых 19 слоев.

Как видно, таблица малообозрима, а при увеличении количества временных слоев вообще становится неудобочитаемой. Результаты расчетов лучше всего представить в виде диаграммы. Для построения диаграммы надо выделить блок А2:L28 и вызвать Мастер Диаграмм. Появится диалог из пяти шагов. На шаге 1 из 5 следует убедиться в том, что выделен блок А2:L28 и щелкнуть по кнопке Шаг>. На шаге 2 из 5 нужно выбрать тип диаграммы - Поверхность. На шаге 3 из 5 выберем формат 1 диаграммы. Далее на шаге 4 из 5 выберем Ряды данных - в строках и в полях Отвести 0 строк введем 1 так, чтобы получилось Отвести 1 строк для меток оси Х. То же самое проделаем для оси Y - Отвести 1 столбцов для меток оси Y. На последнем шаге 5 из 5 в поле Название диаграммы введем текст “Уравнение теплопроводности”, в поле Название по оси категорий(Х) введем текст - “длина”, в поле Значений (Z) - текст”температура”, в поле Рядов (Y) - текст “слой”. Щелкнув по кнопке Закончить, получим диаграмму, примерный вид которой приведен ниже.

Дата добавления: 2014-12-27