Примеры расчета ремонтопригодности

Пример 2.4. Из-за возникших в системе n = 10 отказов на восстановление работоспособности было затрачено 20 ч. Определить доверительный интервал параметра Т _Р с доверительной вероятностью Р (Î) = 0.95 при экспоненциальном распределении времени ремонта.

Решение:

а) определяем среднюю продолжительность ремонта:

;

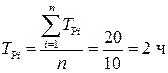б) по таблице 2.4 определяем при n = 10 и Р (Î) = 0.95 r ₁ = 1.83 и r ₂ = 0.64, а затем по формулам (2.21) и (2.22) определяем доверительные границы и интервал I Î изменения:

T _РН = T _Р× r ₂ = 2×0.64 = 1.28 ч;

T _РВ = T _Р× r ₁ = 2×1.83 = 3.66 ч;

I Î = 1.28…3.66 ч.

Ответ: доверительный интервал I Î = 1.28…3.66 ч.

Пример 2.5. Имеется непрерывно работающая двухканальная линия связи. Интенсивность отказа λ и время ремонта канала имеют экспоненциальное распределение с параметром λ= 10^-2 ч^-1 и интенсивностью ремонта μ = 1 ч^-1. Определить среднее значение суммарного времени ремонта линии и доверительный интервал I Î с вероятностью Р (Î) = 0.99 за время эксплуатации 2000 ч. Для восстановления имеется одна бригада. Вероятность отказа двух каналов одновременно Р _1,2 = 0.25. Ремонт отказавшего канала требует выключения всей линии.

Решение:

а) находим наработку на отказ одного канала:

Т ₀ = 1/λ = 1/10^-2 = 100 ч;

б) находим количество отказов в одном из каналов (n ₁или n ₂), суммарное количество отказов в каналах (n _å)и количество отказов одновременно в двух каналах (n _1,2):

n ₁ = n ₂ = t / T ₀ = 2000/100 = 20;

n _å = n ₂ + n ₁ = 20 + 20 = 40;

n _1,2 = n _å× P ₁₂ = 40×0.25 = 10;

в) находим среднее время ремонта:

25% всех отказавших изделий (n _1,2) восстанавливаются поочередно за время:

.

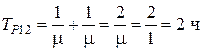Остальные 75% отказавших изделий (N ₁ = n _å - n _1,2 = 40 – 10 = 30) восстанавливаются за время:

T _Р1 = 1/μ = 1/1 = 1 ч.

Среднее время ремонта линии:

;

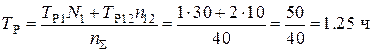г) по таблице 2.4 определяем для n = 40 и Р (Î) = 0.99, что r ₁ = 1.5 и r ₂ = 0.71, а затем по формулам (2.21) и (2.22) определяем доверительные границы и интервал I Î изменения времени ремонта Т _Р:

T _РН = T_Р × r ₂ = 1.25×0.71 = 0.89 ч;

T _РВ = T_Р × r ₁ = 1.25×1.5 = 1.88 ч;

I Î = 0.89…1.88 ч.

Ответ: среднее значение суммарного времени ремонта линии T _Р = 1.25 ч; доверительный интервал I Î = 0.89…1.88 ч.

Пример 2.6. При эксплуатации устройства было зарегистрировано n = 30 отказов. Данные по распределению отказов по группам элементов и времени, затраченному на ремонт, приведены в таблице 2.6. Найти среднее время ремонта устройства и доверительный интервал при Р (Î) = 0.9, если распределение времени ремонта подчиняется закону Эрланга.

Таблица 2.6 – Исходные данные для примера 2.6

Группы элементов	Количество отказов по группе ni	Вес отказов по группе Рi = ni / n	Время ремонта T Р i, мин	Суммарное время ремонта по группе Т å i, мин
Полупроводниковые приборы		0.2	80; 59; 108; 45; 73; 91
Электровакуумные приборы		0.333	56; 36; 44; 42; 33; 32; 23; 75; 61; 28
Микромодули		0.14	26; 34; 19; 23
Резисторы и конденсаторы		0.23	60; 73; 91; 58; 44; 82;
Прочие элементы		0.1	125; 133;

Решение:

а) определяем среднее время ремонта:

- для полупроводниковых приборов:

T _Р1 = 456/6 = 76 мин;

- для электровакуумных приборов (ЭВП):

T _Р2 = 430/10 = 43 мин;

- для микромодулей:

T _Р3 = 102/4 = 25.5 мин;

- для резисторов и конденсаторов:

T _Р4 = 462/7 = 66 мин;

- для прочих элементов:

T _Р5 = 366/3 = 122 мин;

б) рассчитаем среднее время ремонта устройства:

,

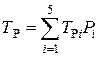где T _{Р i} – среднее время ремонта элементов i -ой группы; Р_i – вес (вероятность) отказов по группам элементов.

Подставляя числовые данные, получим:

T _Р = (76×0.2 + 43×0.33 + 25.5×0.14 + 66×0.23 + 122×0.1)» 60 мин;

в) по таблице 2.5 при n = 30 и Р (Î) = 0.9 находим d₁ = 0.835 и d₂ = 1.22 и с учётом формул (2.24) и (2.25) находим нижнюю и верхнюю доверительные границы времени ремонта Т _Р и доверительный интервал I Î времени ремонта:

T _РН = T _Р/d₂ = 60/1.22 = 49.18 мин;

T _РВ = T _Р/d₁ = 60/0.835 = 71.86 мин;

I Î = 49.18…71.86 мин.

Ответ: среднее время ремонта устройства T _Р = 60 мин; доверительный интервал I Î = 49.18…71.86 мин.

2.2.3 Задачи по расчёту ремонтопригодности

Задача 2.4. На испытание было поставлено N = 50 ремонтируемых устройств. За время испытаний отказало n устройств. Время ремонта T _{Р i} в часах составило: T _Р1 = 4; T _Р2= 3.7; T _Р3= 3.9; T _Р4 = 5.2; T _Р5 = 3.4; T _Р6 = 3.2; T _Р7 = 4.7; T _Р8 = 4.2; T _Р9= 4.5; T _Р10 = 5.3; T _Р11 = 3.1; T _Р12 = 4.4; T _Р13 = 4.8; T _Р14 = 3.8; T _Р15 = 4.6. Определить доверительный интервал времени ремонта T _Р с доверительной вероятностью Р (Î) при заданном законе распределения времени ремонта. Численные значения исходных величин для расчёта даны в таблице 2.7 и зависят от номера варианта. При расчёте использовать первые n цифр T _{Р i}.

Таблица 2.7 – Исходные данные для задачи 2.4

Первая цифра номера варианта
Время ремонта распределено по:	закону Эрланга	экспоненциальному закону
Вторая цифра номера варианта
Р (Î)	0.8	0.9	0.95	0.99	0.8	0.9	0.95	0.99	0.8
Третья цифра номера варианта
n

Задача 2.5. Определить объём испытаний n при условии, что оценка среднего времени ремонта с вероятностью Р (Î) не отличалась бы от верхней доверительной границы более чем в k раз при заданном законе распределения времени ремонта. Вид закона и численные значения исходных величин для расчёта даны в таблице 2.8 и зависят от номера варианта.

Таблица 2.8 – Исходные данные для задачи 2.5

Первая цифра номера варианта
Время ремонта распределено по:	экспоненциальному закону	закону Эрланга
Вторая цифра номера варианта
Р (Î)	0.8	0.9	0.95	0.99	0.8	0.9	0.95	0.99	0.8
Третья цифра номера варианта
k	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.65	1.75

Дата добавления: 2014-12-27