Проведение корреляционного анализа

Корреляционный анализ – это группа статистических методов, направленная на выявление и математическое представление структурных зависимостей между выборками.

Оценку корреляции величин начинают с высказывания гипотезы о возможном характере зависимости между их значениями. Чаще всего допускают наличие линейной зависимости. В таком случае мерой корреляционной зависимости является величина, которая называется коэффициентом корреляции.:

· коэффициент корреляции (обычно обозначаемый греческой буквой ρ) есть число, заключенное в диапазоне от -1 до +1;

· если это число по модулю близко к 1, то имеет место сильная корреляция, если к 0, то слабая;

· близость ρ к +1 означает, что возрастанию одного набора значений соответствует возрастание другого набора, близость к -1 означает обратное;

· значение ρ легко найти с помощью Ехсе1 без всяких формул (разумеется, потому, что в Ехсеl они встроены).

В MS Excel для вычисления парных коэффициентов линейной корреляции используется специальная функция КОРРЕЛ ( массив1; массив2 ), где массив1 – ссылка на диапазон ячеек первой выборки (X); массив2 – ссылка на диапазон ячеек второй выборки (Y).

При большом числе наблюдений, когда коэффициенты корреляции необходимо последовательно вычислять для нескольких выборок, для удобства получаемые коэффициенты сводят в таблицы, называемые корреляционными матрицами.

Корреляционная матрица — это квадратная таблица, в которой на пересечении соответствующих строки и столбца находится коэффициент корреляции между соответствующими параметрами.

В MS Excel для вычисления корреляционных матриц используется процедура Корреляция из пакета Анализ данных. Процедура позволяет получить корреляционную матрицу, содержащую коэффициенты корреляции между различными параметрами.

Для реализации процедуры необходимо:

1. выполнить команду Сервис - Анализ данных;

2.в появившемся списке Инструменты анализа выбрать строку Корреляция и нажать кнопку ОК;

3. в появившемся диалоговом окне указать Входной интервал, то есть ввести ссылку на ячейки, содержащие анализируемые данные. Входной интервал должен содержать не менее двух столбцов.

4. в разделе Группировка переключатель установить в соответствии с введенными данными (по столбцам или по строкам);

5. указать выходной интервал, то есть ввести ссылку на ячейку, с которой будут показаны результаты анализа. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные. Нажать кнопку ОК.

В выходной диапазон будет выведена корреляционная матрица, в которой на пересечении каждых строки и столбца находится коэффициент корреляции между соответствующими параметрами. Ячейки выходного диапазона, имеющие совпадающие координаты строк и столбцов, содержат значение 1, так как каждый столбец во входном диапазоне полностью коррелирует сам с собой.

Рассматривается отдельно каждый коэффициент корреляции между соответствующими параметрами. Отметим, что хотя в результате будет получена треугольная матрица, корреляционная матрица симметрична. Подразумевается, что в пустых клетках в правой верхней половине таблицы нахо­дятся те же коэффициенты корреляции, что и в нижней левой (симметрично расположенные относительно диагонали).

Задание 2. Провести обработкуматрицы результатов тестирования (Тест2) по классической теории тестирования. Выполнять каждый шаг описанного ниже алгоритма в среде Excel.

Классическая теория тестирования

Рассмотрим самые простые и необходимые процедуры статистической обработки результатов тестирования знаний и методы оценки качества теста в соответствии с классической теорией тестирования.

Обозначим через xij числовую оценку успешности выполнения j-го задания, выполненного i-м испытуемым. Результаты тестирования обычно представляются в виде матрицы {xij} с n строками и m столбцами (i=1,…,n; j=1,…,m). В практике тестирования принято, как правило, пользоваться дихотомической шкалой оценок результатов, когда множество возможных оценок состоит всего из двух элементов {0;1}: 0 – задание не выполнено, 1 – выполнено правильно (рис.1).

Рис. 1

Процесс статистической обработки матрицы результатов тестирования будем рассматривать последовательно, по шагам. Ниже рассматриваются эти шаги и приводятся соответствующие формулы. При выполнении этих шагов в среде Ехсе1 можно практически обойтись без формул (разумеется, потому, что в Ехсеl они встроены).

1 шаг. Вычисляются индивидуальные баллы испытуемых yi (i=1,…,n), показывающие результат выполнения теста каждым студентом:

.

Поскольку для проверки статистических гипотез, которые применяются в классической теории тестов, используют предположение о нормальном распределении суммарных баллов испытуемых, то рекомендуется исследовать распределение частот. Для сравнения распределения баллов с нормальным можно использовать любой из критериев, применяемых обычно для этой цели.

2 шаг. Вычисляются средние результаты суммарных баллов испытуемых:

.

3 шаг. Вычисляются средние результаты испытуемых по каждому заданию:

.

Для дихотомических данных величины, вычисляемые по аналогичной формуле, обозначаются через pj и традиционно называются в тестологии мерой трудности задания j (j=1,2,…,m):

.

Заметим, однако, что чем больше величина коэффициента pj, тем большая часть испытуемых успешно справляется с заданием j. Так что на самом деле коэффициенты pj (j=1,2,...,m) должны интерпретироваться как показатели легкости заданий.

4 шаг. Вычисляется дисперсия 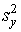и стандартное отклонение суммарных баллов испытуемых:

, .

5 шаг. Вычисляется дисперсия результатов испытуемых по j–ому заданию (j=1,…,m). Если успешность выполнения задания оценивается баллами 0 или 1, мера вариации определяется по формуле:

.

Когда множество оценок состоит из более чем двух значений, применима формула:

.

Вычислив дисперсию, можно найти и стандартное отклонение .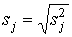

6 шаг. Определяется коэффициент "влияния" тестового задания - связь каждого j–го задания (j=1,…,m) с суммой баллов по всему тесту. Для этого можно использовать коэффициент корреляции Пирсона:

.

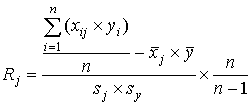Тестовые задания, плохо коррелирующие с суммой баллов (Rj<0,15), должны быть исключены.

7 шаг. Определяется попарная корреляционная связь заданий между собой. Здесь тоже можно использовать коэффициент корреляции Пирсона rjk, (j,k=1, 2,…,m):

.

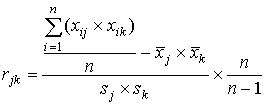Для дихотомических оценок успешности выполнения заданий тот же результат можно получить, оценив эту связь посредством коэффициента корреляции 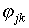(j,k=1, 2,…,m) для такого рода данных:

,

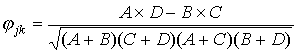где A– количество испытуемых, верно выполнивших задания j и k; B, - количество испытуемых, верно выполнивших задание j и неверно - задание k; C - количество испытуемых, неверно выполнивших задание j и верно задание k; D - количество испытуемых, неверно выполнивших задания j и k. Очевидно, величины A,B,C и D вычисляются по формулам:

, , , .

Тестовые задания, имеющие отрицательные коэффициенты корреляции, должны быть исключены.

8 шаг. Вычисляется индекс Ij(j=1, 2, … m) дискриминативности (дискриминации) задания, то есть его различающая способность, указывающая на возможность разделять отдельных испытуемых по уровню выполнения теста в целом. Для этого из общей совокупности испытуемых выделяют две подгруппы – тех, кто получил самые высокие суммарные баллы, и тех, кто получил самые низкие. Тогда индекс дискриминативности может быть определен как разность между относительными численностями испытуемых, правильно выполнивших задание jв этих двух подгруппах. Например, упорядоченную совокупность суммарных баллов делят на три части и сравнивают результаты выполнения каждого задания j первой и последней третями испытуемых.В этом случае для дихотомических данных индекс приобретает вид:

Чем больше коэффициент Ij, тем больше дискриминативность задания.

Другой способ – вычисление коэффициента дискриминации Dj:

, где

A – множество хорошо успевающих студентов,

B – множество плохо успевающих студентов,
|A| - количество хорошо успевающих студентов.

Дата добавления: 2014-12-27