Методика расчета надежности теста и погрешности измерения тестового балла

Проверка надежности и валидности теста.

Лабораторная работа №8

Цель работы:

• Ознакомиться с основными подходами расчета надежности;
• Научиться рассчитывать надежность и погрешность тестового балла;
• Научиться оценивать валидность тестовых заданий.

Задание 1. Ознакомиться с методикой расчета надежности теста, погрешности измерения тестового балла и оценки валидности тестовых заданий.

1. Общие положения

1.1. Надежность -- это степень повторяемости или степень постоянства эмпирических измерений, т.е. результатов тестирования.

1.2. Надежность теста, отражает точность и устойчивость результатов тестирования к воздействию посторонних случайных факторов. Тест называется надежным, если он дает одни и те же (или очень близкие) показатели для каждого испытуемого при повторном тестировании. Если тест не может дать тот же или близкий результат при повторном испытании для некоторой выборки испытуемых, значит, тест не обладает надежностью. При этом необходимо, чтобы испытуемые не изменили уровень подготовки перед вторым тестированием, и их мотивация к получению наилучших результатов осталась прежней. Надежность связана с понятием стандартной ошибки измерения: чем выше надежность, тем меньше стандартная ошибка измерения.

1.3. На практике обычно рассматриваются два подхода к расчету надежности: ретестовая надежность; надежность расщепленных частей теста.

1.4. Ретестовая надежность - это характеристика надежности педагогического измерения при повторном исследовании результатов испытуемых с помощью одного и того же теста по прошествии некоторого времени. Способ определения ретестовой надежности заключается в вычислении корреляции двух результатов для выборки испытуемых, прошедших тестирования через некоторое время.

1.5. Надежность расщепленных частей теста - это характеристика надежности педагогического измерения, получаемая путем анализа устойчивости результатов отдельных совокупностей тестовых заданий при однократном тестировании. Главным преимуществом этого способа является однократное тестирование.

2. Коэффициент надежности, дисперсия и стандартная ошибка

2.1. Согласно классической теории тестов, развитой в основном на базе нормативно-ориентированного подхода к тестированию, наблюдаемый тестовый балл X состоит из двух компонентов: истинного и ошибочного, что можно выразить в формуле:

X=T+E,

где X - это индивидуальный балл испытуемого; Т - истинный балл испытуемого по данному тесту; Е - ошибочная компонента индивидуального балла.

2.2. Дисперсия наблюдаемых тестовых баллов (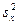) включает дисперсии истинной компоненты () и дисперсии ошибочной компоненты ():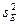

= + .

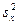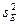Дисперсия тестовых баллов может быть вычислена по формуле:

.

2.3. Надежность теста (коэффициент надежности теста - K) определяется отношением дисперсии истинной компоненты к дисперсии наблюдаемого тестового балла:

Если это отношение близко к нулю, то нормативно-ориентированная интерпретация результатов тестирования ненадежна. Если это отношение приближается к единице, то нормативно-ориентированная интерпретация результатов надежна. Коэффициент надежности должен интерпретироваться не только как характеристика самого теста, но и как характеристика выборки испытуемых и теста.

2.4. Стандартная ошибка измерения рассчитывается как квадратный корень из дисперсии ошибочной компоненты :

.

2.5. Стандартное отклонение рассчитывается, как квадратный корень дисперсии 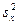наблюдаемых баллов:

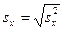. (1)

3. Оценка надежности при повторном тестировании

3.1. Коэффициент надежности рассчитывается на основе коэффициента корреляции между двумя последовательными тестами на одной и той же выборке испытуемых.

3.2. Вычисления надежности теста осуществляется на основе коэффициента корреляции Пирсона между результатами двух тестов:

,(2)

где К - коэффициент надежности теста, 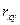- коэффициент корреляции Пирсона, x_i – результат (балл) при первом тестировании i-го испытуемого, y_i – результат (балл) при втором тестировании i- го испытуемого, N – общее количество испытуемых.

3.3. Для вычисления коэффициента надежности по указанной формуле необходимо по результатам двух тестов заполнить таблицу:

Номер студента	Индивидуальный балл по тесту (x)	Индивидуальный балл по тесту (y)	ху	x^2	Y^2
	x1	y1	x1y1	(x1)^2	(y1)^2
	x2	y2	x2y2	(x2)^2	(y1)^2
…	…	…	…	…	…
N	xN	yN	xNyN	(xN)^2	(yN)^2

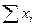
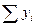
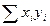
Затем рассчитывается коэффициент надежности по формуле (2).

4. Оценка надежности при однократном тестировнии

4.1.Метод заключается в расщеплении теста на две половины. Для этого весь тест, состоящий из т заданий, разбивают на две половины, чаще всего - на нечетные и четные задания. Отдельно подсчитывают баллы испытуемых для нечетных и четных заданий теста, которые заносят в таблицу:

Номер студента	Индивидуальный балл по нечетным заданиям теста (x)	Индивидуальный балл по четным заданиям теста (y)	ху	x^2	Y^2
	x1	y1	x1y1	(x1)^2	(y1)^2
	X2	y2	x2y2	(x2)^2	(y1)^2
…	…	…	…	…	…
N	xN	yN	xNyN	(xN)^2	(yN)^2

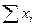
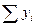
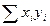
4.2. Коэффициент надежности теста К по двум половинам далее рассчитывается по формуле (2).

4.3. Поскольку коэффициент К - это надежность теста вдвое меньшей длины, где количество заданий равно m/2, то надежность всего теста целиком будет выше, и она находится по формуле Спирмана - Брауна:

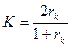
где К - надежность теста в целом; 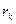- надежности теста по двум половинам.

5. Интерпретация коэффициента надежности теста

Приемлемый коэффициент надежности можно определить с помощью следующей таблицы.

Коэффициент надежности	Оценка надежности
0,9 - 0,99	Отличная
0,8 - 0,89	Хорошая
0,7 - 0,79	Удовлетворительная
менее 0,69	Неудовлетворительная

6. Вычисление погрешности измерения тестового балла

6.1. Зная оценку надежности теста, можно рассчитать стандартную ошибку тестового балла по формуле:

,

где - стандартная погрешность измерения (или стандартная ошибка индивидуального балла испытуемого); К - надежность теста; 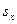- стандартное отклонение индивидуальных баллов в тесте, полученное по формуле (1).

6.2. Доверительный интервал для погрешности измерения тестового балла находится на границах:

,

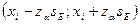где x_i - индивидуальный балл i-го испытуемого, - стандартная погрешность измерения, 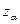- коэффициент, вычисляемый по статистическим таблицам, исходя из принятого уровня надежности , обычно принимается равным 10%, 5% или 1%. Приведем несколько взятых из стандартных таблиц значений этих параметров, которые могут использоваться при расчете.

(%)
	1,28	1,44	1,64	1,96	2,57

6.3. Пример вычисления доверительного интервала для расчета погрешности измерения тестового балла.

Пусть вычислены по приведенным методикам в п.п.2-4 надежность теста К=0,91 и 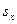=4 - стандартное отклонение индивидуальных баллов в тесте. Испытуемый набрал по тесту 35 баллов из 50 возможных. Тогда при заданном риске допустить ошибку =5%, т.е. в пяти случаев из ста, его истинный бал находится в интервале: или 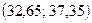. Другими словами, его истинный бал равен: 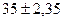. Если схема оценивания – дихотомическая (т.е. за одно ТЗ испытуемый может получить либо 0, либо 1 балл), то истинный балл испытуемого равен: .

Дата добавления: 2014-12-27