Преобразования Галилея

Некоторое неравноправие равноправных систем.

Как уже указывалось в п.5, все инерциальные системы отсчета совершенно равноправны между собой. То есть во всех инерциальных системах все механические процессы протекают одинаково. Это положение называется принципом относительности Галилея.

В 1905 году Эйнштейн пришел к выводу, что этот принцип применим не только к механическим, но и к любым другим явлениям – тепловым, электрическим, оптическим и т.д. Поэтому современная формулировка принципа, носящего имя Эйнштейна и лежащего в основе современного физического мировоззрения, звучит так: во всех инерциальных системах отсчета все явления протекают одинаково.

Однако при совпадении в качественном плане, количественные характеристики многих процессов и явлений, в частности, механических, могут различаться.

Пусть существует инерциальная система отсчета К и движущаяся относительно нее со скоростью 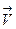другая инерциальная система К ¢ (рис.14). Например, система К – Земля, К ^¢ - вагон поезда. Некоторой неинерциальностью этих систем в данном случае можно пренебречь. Для упрощения рассмотрения примем, что скорость 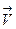направлена вдоль оси абсцисс и оси 0 Х и 0^¢ Х ^¢ совпадают.

Рассмотрим движение некоторого точечного тела А относительно систем К и К ^¢.

Пусть в момент времени t = 0 точки 0 и 0^¢ совпадают, а координаты тела А в обеих системах (0,0,0). К моменту времени t₁ точка 0^¢ передвинется на расстояние 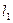от точки 0. Тело А переместится в системе К и в системе К ^¢ и его координаты в системе К будут (х ₁, у ₁, z ₁), а в К ^¢ - (х ¢₁, у ¢₁, z^¢ ₁). При этом:

t₁= t¢₁, у ₁ = у ¢₁, z ₁ = z ¢₁, х ₁ = х ^¢₁+ 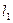= х ^¢₁ + 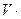×t₁ (34)

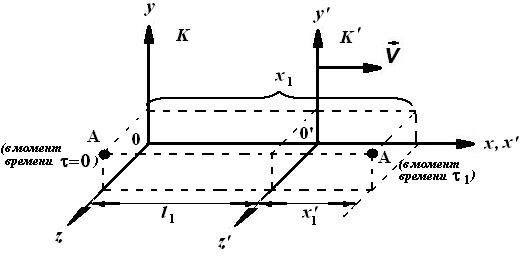
Рис. 14. Различия в описании движения тела по отношению к различным системам отсчета

К моменту времени t₂ координаты тела А будут, соответственно:

(х ₂, у ₂, z ₂), (х ^¢₂, у ^¢₂, z ^¢₂) (35)

и

t₂= t¢₂, у ₂ = у ¢₂, z ₂ = z ¢₂, х = х ¢₂+ 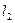= х¢₂ + 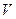t₂ (36)

Таким образом, путь пройденный телом А в системе К ^¢:

D х ^¢ = х ¢₂ - х ¢₁ (37)

и в системе К:

D х = х ₂ - х ₁ =(х ¢₂+ 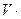t₂) - (х ¢₁+ 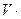t₁) = (х ¢₂ - х ¢₁) + 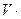(t₂ - t₁) = = D х ¢+ 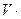Dt, (38)

или: D х ¢= D х - 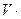Dt. (39)

Следовательно, пути пройденные телом А в системах отсчета К и К ¢ за одно и то же время будут отличаться на (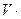 Dt).

Рассмотрим, как пример, движение стюардессы по салону самолета. Допустим, что стюардесса перемещается по салону от хвоста самолета к носу со скоростью 1 м/с (неравномерностью ее движения пренебрегаем). Тогда за 1/3 мин (20 с) она пройдет 20 м. Но самолет, летящий со скоростью 230 м/с (около 830 км/ч) пролетит относительно Земли 4600 м (4,6 км). Таким образом, перемещение стюардессы по отношению к Земле составит (4600 + 20) = 4620 м.

Используя формулу (39), легко показать, что длина тела в разных системах отсчета одинакова. Действительно, поскольку координаты противоположных сторон (концов стержня) измеряются одновременно, то Dt = 0 и

D х ¢= D х. (40)

Используя ту же формулу (39) покажем соотношение между значениями скорости движения тела в системах К и К ¢. Так как скорость рассчитывается как отношение пути, пройденного телом, ко времени движения, то, разделив левую и правую части равенства (39) на Dt, получим:

(41)

u ¢= u - 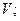или u = u ¢ +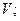

где u, u ¢– соответственно, скорости движения тела относительно систем К и К ¢.^¢

Если движение тела в системе К ^¢ является равнопеременным, т.е. происходит с ускорением 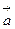, то на основании формулы (41) получаем значение ускорения тела в системе К. При этом следует помнить, что скорость движения 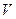одной системы относительно другой является постоянной, так как обе системы инерциальны. Тогда, разделив изменение скоростей на время, получаем:

,

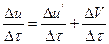а так как V= const и, следовательно, D V = 0, то

a =a ¢ (42)

Таким образом, есть параметры значения, которых в разных инерциальных системах отсчета одинаковы (длина, ускорение). Но такие параметры как координаты, пройденный путь, скорость в разных инерциальных системах отсчета будут иметь разные значения.

Дата добавления: 2014-12-27